 por Raphael Feitas10 » Qui Jan 12, 2012 01:49
por Raphael Feitas10 » Qui Jan 12, 2012 01:49
Quatro rapazes compraram um objeto por $ 60,00. O primeiro rapaz pagou a metada da soma do valor pago pelos outros rapazes; o segundo rapaz pagou um terço da soma do valor pago pelos outros rapazes; o terceiro rapaz pagou um quarto da soma do valor pago pelos outros rapazes.Calcule quanto pagou o quarto rapaz.R: $ 13,00
Brother eu conseguie montar ela mais quando fui fazer me compliquei todinho me ajuda aew parceiro desde de já muito agradecido...
Montei ela assim saca aew...
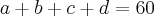


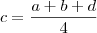

mas quando fui jogar uma dentro da outra para deixar uma variavel só e achar a resposta ñ conseguie ver oq vc pode fazer aew brother...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por ant_dii » Qui Jan 12, 2012 02:55
por ant_dii » Qui Jan 12, 2012 02:55
Você fez tudo certo, mas não precisa deixar numa variável só de uma única vez.
Veja, considerando que
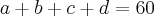
e as condições para o primeiro é que

então
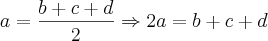
,
de onde
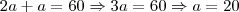
O mesmo para

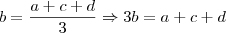
,
de onde
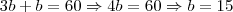
e para
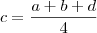

,
de onde

.
Agora basta substituir em
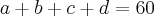
os valores respectivos e encontrará a resposta para

...
Valew??
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Raphael Feitas10 » Qui Jan 12, 2012 13:11
por Raphael Feitas10 » Qui Jan 12, 2012 13:11
Nossa brother ñ sabia q era tão simples assim ñ vacilo mais numa dessa muito obrg por ter me ajudado valeu mesmo.
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- números inteiros
por thadeu » Qui Nov 19, 2009 11:41
- 2 Respostas
- 2070 Exibições
- Última mensagem por thadeu

Qui Nov 19, 2009 13:46
Álgebra Elementar
-
- numeros inteiros
por edwilsoncrep » Qui Mar 04, 2010 20:03
- 5 Respostas
- 6390 Exibições
- Última mensagem por adriana_borges

Dom Mai 09, 2010 12:04
Sequências
-
- Numeros inteiros
por Raphael Feitas10 » Qua Jan 05, 2011 00:16
- 3 Respostas
- 2683 Exibições
- Última mensagem por PedroSantos

Qua Jan 05, 2011 19:49
Cálculo: Limites, Derivadas e Integrais
-
- Numeros inteiros
por Raphael Feitas10 » Qui Jan 13, 2011 13:18
- 15 Respostas
- 9695 Exibições
- Última mensagem por Raphael Feitas10

Qua Jan 19, 2011 00:40
Números Complexos
-
- Numeros inteiros 2
por Raphael Feitas10 » Qua Jan 19, 2011 00:28
- 1 Respostas
- 2893 Exibições
- Última mensagem por Renato_RJ

Qua Jan 19, 2011 01:52
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
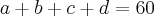


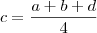



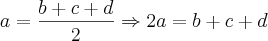 ,
,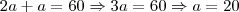
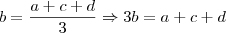 ,
,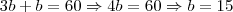
 ,
, .
. ...
...