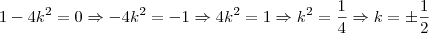por gicapo » Seg Jan 09, 2012 21:12
por gicapo » Seg Jan 09, 2012 21:12
Já agora Renato precisava se conseguisses a resolução de :
Calcule a derivada total de f(x,y)=x^2+4y^2
Quando
x(t)=sin(alfat), y(t)= €cos(alfat)
onde alfa,€, são números reais positivos.
Diaga ainda se existe algum valor de € para o qual a derivada total se anula para todo o t. Se existir, calcule esse valor (ou um deles, se não for único).
-
gicapo
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 09, 2012 09:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão
- Andamento: cursando
 por Renato_RJ » Ter Jan 10, 2012 05:48
por Renato_RJ » Ter Jan 10, 2012 05:48
Boa noite Gicapo !!
Vou fazer apenas uma modificação, vou mudar o símbolo que você colocou em

para k, então o exercício ficará assim (sem alteração no resultado final, é só uma mudança de nome):

Onde:
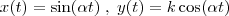
Como você pede a derivada total de

, vou considerar que você deseje derivar a função f em relação a variável t, então temos o caso seguinte:

Onde:

Substituindo na equação (1), temos:
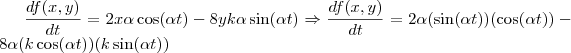
O que nos dá:

Colocando

em evidência, temos:

O valor para k tal que a derivada total se anule é aquele que leva a equação

a zero, achemos as raízes dessa equação:
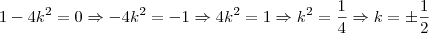
Espero não ter cometido algum engano...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por gicapo » Qua Jan 11, 2012 10:18
por gicapo » Qua Jan 11, 2012 10:18
Renato_RJ escreveu:Boa noite Gicapo !!
Vou fazer apenas uma modificação, vou mudar o símbolo que você colocou em

para k, então o exercício ficará assim (sem alteração no resultado final, é só uma mudança de nome):

Onde:
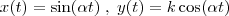
Como você pede a derivada total de

, vou considerar que você deseje derivar a função f em relação a variável t, então temos o caso seguinte:

Onde:

Substituindo na equação (1), temos:
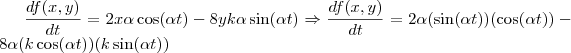
O que nos dá:

Colocando

em evidência, temos:

O valor para k tal que a derivada total se anule é aquele que leva a equação

a zero, achemos as raízes dessa equação:
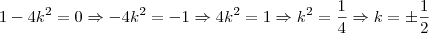
Espero não ter cometido algum engano...
[ ]'s
Renato.
MUITO OBRIGADO RENATO
-
gicapo
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 09, 2012 09:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequações
por Bruno 888 » Qua Set 24, 2008 20:36
- 1 Respostas
- 4203 Exibições
- Última mensagem por admin

Ter Set 30, 2008 17:09
Inequações
-
- Inequações
por Rose » Seg Nov 24, 2008 22:44
- 2 Respostas
- 3689 Exibições
- Última mensagem por Rose

Qua Nov 26, 2008 08:18
Inequações
-
- Inequações
 por cristina » Seg Set 07, 2009 01:46
por cristina » Seg Set 07, 2009 01:46
- 2 Respostas
- 2915 Exibições
- Última mensagem por cristina

Seg Set 07, 2009 20:55
Sistemas de Equações
-
- inequações
por jose henrique » Ter Out 26, 2010 23:56
- 10 Respostas
- 6806 Exibições
- Última mensagem por MarceloFantini

Qui Nov 04, 2010 10:31
Sistemas de Equações
-
- Inequações
por brijahh » Sáb Ago 06, 2011 10:38
- 1 Respostas
- 2197 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 06, 2011 17:00
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 para k, então o exercício ficará assim (sem alteração no resultado final, é só uma mudança de nome):
para k, então o exercício ficará assim (sem alteração no resultado final, é só uma mudança de nome):
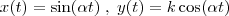
 , vou considerar que você deseje derivar a função f em relação a variável t, então temos o caso seguinte:
, vou considerar que você deseje derivar a função f em relação a variável t, então temos o caso seguinte:

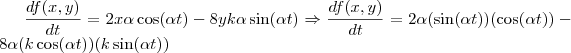

 em evidência, temos:
em evidência, temos:
 a zero, achemos as raízes dessa equação:
a zero, achemos as raízes dessa equação: