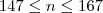 . Dividindo esse alunos em grupos de 4, sobram dois deles e, dividindo-os em grupos de 6, também sobram dois alunos. Calcule o valor de n.
. Dividindo esse alunos em grupos de 4, sobram dois deles e, dividindo-os em grupos de 6, também sobram dois alunos. Calcule o valor de n.A resposta é 158. Entretanto, não consegui pensar em um caminho para resolvê-la.
Agradeço a quem ajudar.

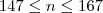 . Dividindo esse alunos em grupos de 4, sobram dois deles e, dividindo-os em grupos de 6, também sobram dois alunos. Calcule o valor de n.
. Dividindo esse alunos em grupos de 4, sobram dois deles e, dividindo-os em grupos de 6, também sobram dois alunos. Calcule o valor de n.
Arkanus Darondra escreveu:Numa turma, há n alunos, com. Dividindo esse alunos em grupos de 4, sobram dois deles e, dividindo-os em grupos de 6, também sobram dois alunos. Calcule o valor de n.
A resposta é 158. Entretanto, não consegui pensar em um caminho para resolvê-la.
Agradeço a quem ajudar.
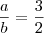
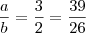
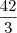 )...
)...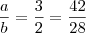
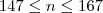



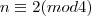 e
e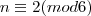 .
.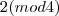 , isto é aqueles
, isto é aqueles  que deixam resto 2 na divisão por 4 são 150, 154, 158, 162 e 166.
que deixam resto 2 na divisão por 4 são 150, 154, 158, 162 e 166.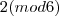 , isto é aqueles
, isto é aqueles  que deixam resto 2 na divisão por 6 são 152, 158 e 164.
que deixam resto 2 na divisão por 6 são 152, 158 e 164.


Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
