Sejam
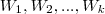 subespaços de um espaço vetorial
subespaços de um espaço vetorial  .
.Mostre que

onde
 é o subespaço gerado pela união finita dos subespaços
é o subespaço gerado pela união finita dos subespaços 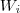
e
 {
{  }.
}.Agradeço desde já.

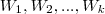 subespaços de um espaço vetorial
subespaços de um espaço vetorial  .
.
 é o subespaço gerado pela união finita dos subespaços
é o subespaço gerado pela união finita dos subespaços 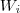
 {
{  }.
}.
nietzsche escreveu:Sejam,
, ...,
subespaços de um espaço vetorial V.
Mostre que
ondeé o subespaço gerado pela união finita dos subespaços
e.
 , devemos provar que para todo
, devemos provar que para todo  , temos que
, temos que  .
.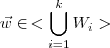 .
.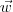 pertence a união de todos os
pertence a união de todos os  (com i=1, 2, ..., k), então ele pertence a pelo menos um desses conjuntos.
(com i=1, 2, ..., k), então ele pertence a pelo menos um desses conjuntos.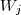 , sendo
, sendo  . Ou seja, suponha que temos
. Ou seja, suponha que temos  .
. , temos que
, temos que  , já que podemos escrever:
, já que podemos escrever: , lembrando que
, lembrando que  com i=1, 2, ..., j-1, j+1, ..., k.
com i=1, 2, ..., j-1, j+1, ..., k.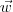 escolhido foi qualquer, podemos concluir que:
escolhido foi qualquer, podemos concluir que:


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.



