 por Raphael Feitas10 » Seg Jan 09, 2012 17:28
por Raphael Feitas10 » Seg Jan 09, 2012 17:28
Um homem bebe 1/3 de um copo de vinho.Encheu de agua e bebe a metade do copo cheio, enche-o a segunda vez e bebe a metade do copo cheio.Calcular que fração de vinho fica no copo.R: 1/6
Brother fiz assim mais ñ fiquei satisfeito desse jeito q eu fiz ñ se eu tiver errado me corrija aew por favor desde ja agradecido.
![\frac{x}{3}+\frac{x}{2}+\frac{x}{2}=\frac{2x+3x+3x}{6}[/te[tex] \frac{x}{3}+\frac{x}{2}+\frac{x}{2}=\frac{2x+3x+3x}{6}[/te[tex]](/latexrender/pictures/d6fc06de4e71758eb4e33d7e6109bf49.png)
aew agora só fiz subtrair a fração que corresponde a agua e a do vinho que é
![\frac{3}{6}-\frac{2}{6}=\frac{1}{6}[/tex[tex] \frac{3}{6}-\frac{2}{6}=\frac{1}{6}[/tex[tex]](/latexrender/pictures/06e7a00542be8edc37455b8f8f96ec4e.png)
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Arkanus Darondra » Seg Jan 09, 2012 18:43
por Arkanus Darondra » Seg Jan 09, 2012 18:43
Raphael Feitas10 escreveu:Brother fiz assim mais ñ fiquei satisfeito desse jeito q eu fiz ñ se eu tiver errado me corrija aew por favor desde ja agradecido.


corresponde à quantidade de vinho que ele bebeu

já corresponde à quantidade de líquido no copo que ele bebeu (não especificamente somente de vinho)
Raphael Feitas10 escreveu:Um homem bebe 1/3 de um copo de vinho.
Um copo cheio de vinho tem

de vinho
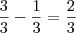
Raphael Feitas10 escreveu:Encheu de agua e bebe a metade do copo cheio
Então ele bebe metade do vinho que tinha sobrado, sobrando

Raphael Feitas10 escreveu:enche-o a segunda vez e bebe a metade do copo cheio.Calcular que fração de vinho fica no copo
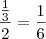
Ou então
Total de vinho:

Total de água colocada:


Espero ter ajudado.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3800 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- fração
por leandro moraes » Qui Jan 14, 2010 19:41
- 1 Respostas
- 1688 Exibições
- Última mensagem por MarceloFantini

Qui Jan 14, 2010 20:09
Estatística
-
- Fração
por bia rosendo » Seg Jun 06, 2011 11:45
- 2 Respostas
- 4506 Exibições
- Última mensagem por Claudin

Seg Jun 06, 2011 18:34
Matemática Financeira
-
- Fração 112
por Raphael Feitas10 » Sex Jan 13, 2012 02:23
- 1 Respostas
- 1668 Exibições
- Última mensagem por ant_dii

Sex Jan 13, 2012 03:18
Sistemas de Equações
-
- Fracão
por Yasmin Felix » Sáb Jan 14, 2012 13:34
- 3 Respostas
- 2161 Exibições
- Última mensagem por marques_gc

Sáb Jan 14, 2012 14:14
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{x}{3}+\frac{x}{2}+\frac{x}{2}=\frac{2x+3x+3x}{6}[/te[tex] \frac{x}{3}+\frac{x}{2}+\frac{x}{2}=\frac{2x+3x+3x}{6}[/te[tex]](/latexrender/pictures/d6fc06de4e71758eb4e33d7e6109bf49.png)
![\frac{3}{6}-\frac{2}{6}=\frac{1}{6}[/tex[tex] \frac{3}{6}-\frac{2}{6}=\frac{1}{6}[/tex[tex]](/latexrender/pictures/06e7a00542be8edc37455b8f8f96ec4e.png)

![\frac{x}{3}+\frac{x}{2}+\frac{x}{2}=\frac{2x+3x+3x}{6}[/te[tex] \frac{x}{3}+\frac{x}{2}+\frac{x}{2}=\frac{2x+3x+3x}{6}[/te[tex]](/latexrender/pictures/d6fc06de4e71758eb4e33d7e6109bf49.png)
![\frac{3}{6}-\frac{2}{6}=\frac{1}{6}[/tex[tex] \frac{3}{6}-\frac{2}{6}=\frac{1}{6}[/tex[tex]](/latexrender/pictures/06e7a00542be8edc37455b8f8f96ec4e.png)

 corresponde à quantidade de vinho que ele bebeu
corresponde à quantidade de vinho que ele bebeu já corresponde à quantidade de líquido no copo que ele bebeu (não especificamente somente de vinho)
já corresponde à quantidade de líquido no copo que ele bebeu (não especificamente somente de vinho) de vinho
de vinho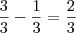

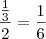





 .
.
 :
: