 por Arkanus Darondra » Qua Dez 28, 2011 19:45
por Arkanus Darondra » Qua Dez 28, 2011 19:45
Alguém poderia me ajudar na resolução desta questão?
A expressão

, se for simplicada, vamos obter:
O gabarito é:

Obs: Tentei colocar xy em evidência tanto no numerador quanto no denominador e simplificar

E apliquei a diferença de cubos no denominador
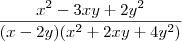
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Qua Dez 28, 2011 21:35
por fraol » Qua Dez 28, 2011 21:35
Olá Arkanus,
Sua fatoração está correta, para completá-la, basta colocar (x-y) em evidência no numerador que se chega ao resultado. Quer tentar?
Obs: Colocar (x-y) significa dividir o polinômio do numerador por (x-y).
Valeu,
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Arkanus Darondra » Qua Dez 28, 2011 22:14
por Arkanus Darondra » Qua Dez 28, 2011 22:14
fraol escreveu:Olá Arkanus,
Sua fatoração está correta, para completá-la, basta colocar (x-y) em evidência no numerador que se chega ao resultado. Quer tentar?
Obs: Colocar (x-y) significa dividir o polinômio do numerador por (x-y).
Valeu,
Francisco.
Fraol,
Deu certo aqui. Valeu
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Arkanus Darondra » Sáb Jan 07, 2012 19:13
por Arkanus Darondra » Sáb Jan 07, 2012 19:13
Já faz um tempo que esta dúvida foi respondida, e, inclusive, além da divisão proposta resolvi da seguinte maneira:

Gostaria de saber como é possível saber por qual polinômio eu devo dividir para chegar a fatoração, como, por exemplo, neste caso que foi por (x - y).
e se há casos que só será possível fatorar pelo método da divisão de polinômio.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Jan 07, 2012 19:27
por DanielFerreira » Sáb Jan 07, 2012 19:27
Arkanus,
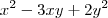
pode ser fatorada como uma eq. do 2º!
Assim como vc a fez.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Arkanus Darondra » Sáb Jan 07, 2012 19:42
por Arkanus Darondra » Sáb Jan 07, 2012 19:42
danjr5, minha dúvida, na verdade, são estas duas:
- Como é possível saber por qual polinômio dividir para se fatorar? Como, no caso (x - y), que o fraol disse acima.
- Existe algum caso em que só é possível fatorar por meio da divisão de polinômios e não como deste último ("quebrando o polinômio")?
Agradeço a quem me responder.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Jan 07, 2012 20:14
por DanielFerreira » Sáb Jan 07, 2012 20:14
- Como é possível saber por qual polinômio dividir para se fatorar? Como, no caso (x - y), que o fraol disse acima.
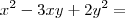
Trata-se de um trinômio que pode ser fatorado como uma equação do 2º.
Ex:
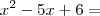


Isto é,
devemos encontrar dois números (solução) cuja soma seja 5 e o produto 6.
São eles: 2 e 3.
trocando os sinaisdaí,
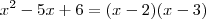
Voltando a questão:


São eles: 1 e 2.
trocando os sinaisdaí,
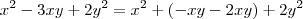
 agrupamento
agrupamento"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Sáb Jan 07, 2012 20:15
por DanielFerreira » Sáb Jan 07, 2012 20:15
- Existe algum caso em que só é possível fatorar por meio da divisão de polinômios e não como deste último ("quebrando o polinômio")?
Nesse caso, deixaria de ser fatoração!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Arkanus Darondra » Sáb Jan 07, 2012 21:25
por Arkanus Darondra » Sáb Jan 07, 2012 21:25
Obrigado.
Para
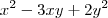
Achei

e

, logo as raízes são

e

Então, apliquei
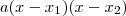
chegando à

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Jan 07, 2012 22:04
por DanielFerreira » Sáb Jan 07, 2012 22:04
Arkanus Darondra escreveu:Obrigado.
Para
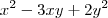
Achei

e

, logo as raízes são

e

Então, apliquei
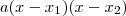
chegando à

Arkanus,
já que sabia como fatorar, poderia detalhar mais sua dúvida?
Arkanus escreveu:- Como é possível saber por qual polinômio dividir para se fatorar? Como, no caso (x - y), que o fraol disse acima.
Não ficou clara!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Arkanus Darondra » Sáb Jan 07, 2012 22:18
por Arkanus Darondra » Sáb Jan 07, 2012 22:18
Quanto à minha última resposta, apenas pude fazer os cálculos observando a sua explicação.
Quanto à outra pergunta que fiz:
Como é possível saber por qual polinômio dividir para se fatorar? Como, no caso (x - y), que o fraol disse acima.Eu quis saber como o fraol sabia que dividindo o polinômio
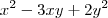
por

a questão seria resolvida (como se pode notar na primeira resposta deste tópico).
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Jan 08, 2012 16:02
por DanielFerreira » Dom Jan 08, 2012 16:02
vlw.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fatoração e simplificação de polinomios
 por arg1209 » Ter Jun 10, 2014 15:55
por arg1209 » Ter Jun 10, 2014 15:55
- 1 Respostas
- 2261 Exibições
- Última mensagem por alienante

Dom Jun 15, 2014 17:26
Polinômios
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2351 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [Simplificação]Fazer a simplificação da resposta
por neoreload » Qua Fev 04, 2015 05:50
- 3 Respostas
- 2867 Exibições
- Última mensagem por neoreload

Sáb Fev 07, 2015 22:10
Equações
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8909 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3256 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , se for simplicada, vamos obter:
, se for simplicada, vamos obter:

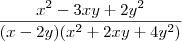

 , se for simplicada, vamos obter:
, se for simplicada, vamos obter:

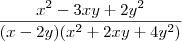





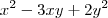 pode ser fatorada como uma eq. do 2º!
pode ser fatorada como uma eq. do 2º!

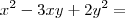
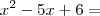


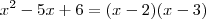


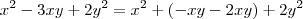



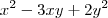
 e
e  , logo as raízes são
, logo as raízes são  e
e 
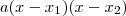 chegando à
chegando à 

e
, logo as raízes são
e
chegando à

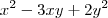 por
por 




 , avisa que eu resolvo.
, avisa que eu resolvo.

