Sub-seção para materiais das disciplinas relacionadas à Geometria.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por andersontricordiano » Ter Out 04, 2011 18:23
por andersontricordiano » Ter Out 04, 2011 18:23
As dimensões de um bloco retangular de diagonal
![\sqrt[]{371} \sqrt[]{371}](/latexrender/pictures/953ef55059ca9d7643d52a8dec481d16.png)
cm são expressas por números ímpares consecutivos.
a)Qual o volume do bloco?
b)Qual é o volume de um segundo bloco cujas dimensões são 20% menores que as dimensões do primeiro bloco?
Respostas:
a)1287 cm³
b)658,944 cm³
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Arkanus Darondra » Qui Jan 05, 2012 02:32
por Arkanus Darondra » Qui Jan 05, 2012 02:32
andersontricordiano escreveu:As dimensões de um bloco retangular de diagonal
![\sqrt[]{371} \sqrt[]{371}](/latexrender/pictures/953ef55059ca9d7643d52a8dec481d16.png)
cm são expressas por números ímpares consecutivos.
a)Qual o volume do bloco?
As dimensões são número ímpares consecutivos, logo, podemos representá-las como sendo
x, (x + 2) e (x + 4)
A diagonal desse bloco, corresponde a seguinte equação
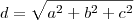
, ou seja,

Então temos que

Admitindo somente a solução positiva da equação encontrada para os valores das dimensões do bloco,
e por meio da equação do volume do mesmo

, chega-se à resposta.
andersontricordiano escreveu:b)Qual é o volume de um segundo bloco cujas dimensões são 20% menores que as dimensões do primeiro bloco?
Basta multiplicarmos as dimensões encontradas no item anterior por 0,8, e proceder da mesma forma.
Abraço

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- questão - geometria - bloco de madeira
por leo_30_rj » Seg Jul 26, 2010 03:25
- 2 Respostas
- 2643 Exibições
- Última mensagem por leo_30_rj

Ter Jul 27, 2010 02:11
Geometria Espacial
-
- Calculo com Geometria Analitica volume 2.
por 380625 » Dom Jul 10, 2011 13:28
- 2 Respostas
- 6135 Exibições
- Última mensagem por 380625

Dom Jul 10, 2011 16:49
Pedidos de Materiais
-
- Qual é o elemento de volume no caso de integrais triplas?
 por Guga1981 » Sáb Jul 25, 2020 11:18
por Guga1981 » Sáb Jul 25, 2020 11:18
- 0 Respostas
- 6129 Exibições
- Última mensagem por Guga1981

Sáb Jul 25, 2020 11:18
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo do Volume] Variação do volume em porcentagem
por Douglaasag » Sex Out 10, 2014 09:23
- 0 Respostas
- 4474 Exibições
- Última mensagem por Douglaasag

Sex Out 10, 2014 09:23
Cálculo: Limites, Derivadas e Integrais
-
- [Centro de gravidade] Bloco homogeneo em repouso plano incli
por gustavoluiss » Seg Nov 07, 2011 07:54
- 5 Respostas
- 4762 Exibições
- Última mensagem por Neperiano

Seg Nov 07, 2011 15:39
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{371} \sqrt[]{371}](/latexrender/pictures/953ef55059ca9d7643d52a8dec481d16.png) cm são expressas por números ímpares consecutivos.
cm são expressas por números ímpares consecutivos.
![\sqrt[]{371} \sqrt[]{371}](/latexrender/pictures/953ef55059ca9d7643d52a8dec481d16.png) cm são expressas por números ímpares consecutivos.
cm são expressas por números ímpares consecutivos.
cm são expressas por números ímpares consecutivos.
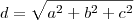 , ou seja,
, ou seja,

 , chega-se à resposta.
, chega-se à resposta.

