 por Adriana Barbosa » Ter Mai 26, 2009 23:39
por Adriana Barbosa » Ter Mai 26, 2009 23:39
Dado um pedaço de papelão quadrado com 8 cm de lado, tira-se de cada canto do papelão, quadrados com x cm de lados e os bordos são dobrados de modo que forme uma caixa sem tampa. Determine:
(a) O volume V da caixa em função de x;
(b) A área S da caixa em função de x.
Por favor poderia me dizer algumas dicas de como poderia resolver esta questão?
Estou sem

!
Por favor me ajude!

-
Adriana Barbosa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 26, 2009 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 23:55
por Molina » Ter Mai 26, 2009 23:55
Primeiramente vamos tentar resolver a letra a)
Sugiro que você monte um esboço do que o problema quer. Você já conseguiu interpretá-lo?
Depois disso, você precisa usar o volume de um paralelepípedo, que é:
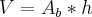
, onde
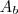
é a área da base e

é a altura.
Experimente pegar x como 1, 2, 3 e veja qual resultado quer. Pegar x como esses valores, significa que você irá cortar nas pontas um quadrado de lado 1, 2 e 3 e irá sobrar as partes que sobraram, formando, como o enunciado diz, uma caixa sem tampa.
Tente aí e depois me diga onde você chegou..
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Adriana Barbosa » Qua Mai 27, 2009 00:23
por Adriana Barbosa » Qua Mai 27, 2009 00:23
Ainda não estou conseguindo!
Criei um esboço, se seria desta forma que estou pensando! Esta anexado no arquivo!
Obrigada, pela atenção e pela paciência!
- Anexos
-

- esboço, matemática.jpg (5.69 KiB) Exibido 2468 vezes
-
Adriana Barbosa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 26, 2009 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Molina » Qua Mai 27, 2009 00:46
por Molina » Qua Mai 27, 2009 00:46
Fiz uma nova figura para ve se voce visualiza melhor.
Tente entender o valor que eu coloquei a cada lado.
A área pintada de cinza significa a área da base. Quanto ela vale?
Boas tentativas,

- Anexos
-
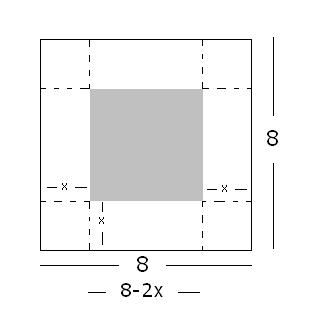
- caixa.JPG (8.14 KiB) Exibido 2463 vezes
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5565 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4587 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5738 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3483 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2948 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 !
!

 !
!

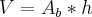 , onde
, onde 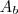 é a área da base e
é a área da base e  é a altura.
é a altura.





 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.