Sou novo aqui, e pra começar, queria tentar compartilhar uma dúvida com vocês...
Eu tenho uma prova, para fazer na sexta feira, e a matéria é sobre quadriláteros.
Só que o problema, é que por mais que eu tente, não consigo fazer nenhum exercício!
EX¹:
73) Sabendo que ABCD é um trapézio e que os segmentos com marcas iguais são congruentes, determine os valores das ingógnitas:
Dai, aparece a imagem de um trapézio, divido em 4 partes:

Só que eu não consigo resolver...
Não sei nem por onde começar...
Minha matéria vai de quadriláteros, trapézio retângulo, ângulos congruentes...
Só que isso não entra na minha cabeça!
Não é falta de vontade, só em matemática minhas médias não são boas...
Nas outras não cai de 8...
Por favor, me ajudem...


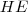 é base média do trapézio
é base média do trapézio 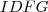
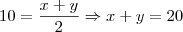
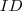 é base média do trapézio
é base média do trapézio 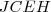
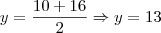

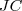 é base média do trapézio
é base média do trapézio 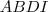
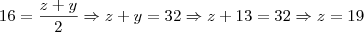

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.