 por TiagoFERD » Sex Dez 30, 2011 17:42
por TiagoFERD » Sex Dez 30, 2011 17:42
Boa noite! mais um problema que está me matando!
seja então:
Determine se é linear a aplicação : F : R3 ---> R2
F(x,y,z) = (y,0)
resolução:
1. F(p1+p2) = f(p1) + f(p2)
2. F (Kp1) = KF(p1)
1. p1= (x,y,z)
p2= (x´,y´z´)
p1+p2 = (x+x´,y+y´,z+z´)
F(p1) (y,0)
F(p2) (y´,0)
1. F ( p1+p2) = F(p1)+ F(p2)
F(p1+P2)= y+y´,0) e F(p1)+F(p2) = (y+y´0+0) verificado?
2. falha na multiplicação do escalar por causa do 0?
Muito Obrigado.
-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por TheoFerraz » Sex Dez 30, 2011 19:30
por TheoFerraz » Sex Dez 30, 2011 19:30
A primeira está sim verificada.
e quanto a segunda... não da falha não... mesmo no zero... se voce multiplicar
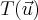
por zero voce obtém a (000) e se voce aplicar na transformação um vetor qualquer multiplicado por zero (que vai resultar em (000)) voce obtém (000) ainda sim.
Essa transformação é linear!
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por TiagoFERD » Sex Dez 30, 2011 20:15
por TiagoFERD » Sex Dez 30, 2011 20:15
TheoFerraz escreveu:A primeira está sim verificada.
e quanto a segunda... não da falha não... mesmo no zero... se voce multiplicar
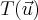
por zero voce obtém a (000) e se voce aplicar na transformação um vetor qualquer multiplicado por zero (que vai resultar em (000)) voce obtém (000) ainda sim.
Essa transformação é linear!
tem razão! eu não olhei bem a solução! perdi muito tempo tentando ver se não era linear :(.
tenho algumas demonstrações para provar de outro exercício, mas não sei se tá bem provado, mais logo vou postar! se puderes ajudar eu agradecia muito!
Obrigado e desde já um excelente ano de 2012

-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8151 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10526 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11558 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13597 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- aplicaçao de EDO
por nayana_ac » Dom Set 19, 2010 01:28
- 3 Respostas
- 15278 Exibições
- Última mensagem por Krilitolxc

Ter Fev 02, 2016 07:40
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


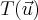 por zero voce obtém a (000) e se voce aplicar na transformação um vetor qualquer multiplicado por zero (que vai resultar em (000)) voce obtém (000) ainda sim.
por zero voce obtém a (000) e se voce aplicar na transformação um vetor qualquer multiplicado por zero (que vai resultar em (000)) voce obtém (000) ainda sim.


 , avisa que eu resolvo.
, avisa que eu resolvo.

