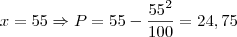por [NewtoN] » Qua Dez 28, 2011 11:24
por [NewtoN] » Qua Dez 28, 2011 11:24
Uma loja está fazendo uma promoção na venda de balas: "Compre x balas e ganhe x% de desconto". A promoção é válida pra compras de até 60 balas, caso em que é concedido o desconto máximo de 60%. Alfredo, Beatriz, Carlos e Daniel compraram 10, 15, 30 e 45 balas, respectivamente. Qual deles poderia ter comprado mais balas e gasto a mesma quantia, se empregasse melhor seus conhecimentos de matemética ?
a)Alfredo
b)Beatriz
c)Carlos
d)Daniel
e)Nenhum
-
[NewtoN]
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Dez 21, 2011 11:47
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Qui Dez 29, 2011 01:39
por Renato_RJ » Qui Dez 29, 2011 01:39
Boa noite, tudo em paz ???
Seguinte, podemos representar essa promoção matematicamente da seguinte forma (veja que o problema diz "compre x balas e ganhe x% de desconto"):
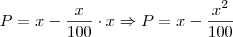
Logo a quantia a ser paga pelas balas será
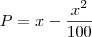
, mas o problema pede para descobrirmos como comprar mais balas gastando menos, logo temos um problema de máximo, como temos uma função de segundo grau com coeficiente líder negativo (o valor que multiplica o x de maior grau), logo o vértice da parábola descrita pela função achada representa o máximo da função, logo:
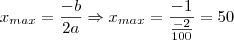
Logo, a quantidade que tem o maior desconto é de 50 balas. Agora, repare que Daniel poderia ter comprado 55 balas pelo mesmo preço que pagou pelas 45, veja:
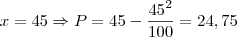
Agora vejamos com
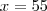
:
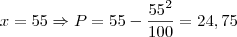
Então a resposta desejada é Daniel, pois ele poderia ter comprado 55 balas (10 balas a mais do que realmente comprou) pelo mesmo preço.
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por [NewtoN] » Ter Jan 03, 2012 21:47
por [NewtoN] » Ter Jan 03, 2012 21:47
Muito obrigado Renato. Muito bem explicado.
Abraços
-
[NewtoN]
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Dez 21, 2011 11:47
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvida de questao mat.financeira
por hvgui » Ter Jun 18, 2013 19:05
- 0 Respostas
- 1375 Exibições
- Última mensagem por hvgui

Ter Jun 18, 2013 19:05
Matemática Financeira
-
- QUESTÃO DE MATEMÁTICA FINANCEIRA COM LOGARÍTIMOS
por saulfiterman » Seg Ago 20, 2012 21:26
- 1 Respostas
- 3490 Exibições
- Última mensagem por LuizAquino

Seg Set 24, 2012 10:50
Logaritmos
-
- Matemática Financeira - Questão com Porcentagem
por joedsonazevedo » Qui Nov 08, 2012 14:50
- 6 Respostas
- 6768 Exibições
- Última mensagem por saberdigitalnet

Sáb Nov 24, 2012 21:01
Matemática Financeira
-
- [Matematica Financeira] Questão desafio
por CARLOS POVOAS » Qua Jun 19, 2013 00:35
- 0 Respostas
- 1797 Exibições
- Última mensagem por CARLOS POVOAS

Qua Jun 19, 2013 00:35
Matemática Financeira
-
- Matemátia Financeira - Dúvida
por carol1112 » Seg Abr 15, 2013 22:34
- 5 Respostas
- 2947 Exibições
- Última mensagem por carol1112

Ter Abr 16, 2013 21:22
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


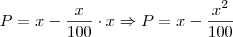
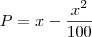 , mas o problema pede para descobrirmos como comprar mais balas gastando menos, logo temos um problema de máximo, como temos uma função de segundo grau com coeficiente líder negativo (o valor que multiplica o x de maior grau), logo o vértice da parábola descrita pela função achada representa o máximo da função, logo:
, mas o problema pede para descobrirmos como comprar mais balas gastando menos, logo temos um problema de máximo, como temos uma função de segundo grau com coeficiente líder negativo (o valor que multiplica o x de maior grau), logo o vértice da parábola descrita pela função achada representa o máximo da função, logo: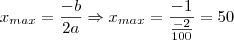
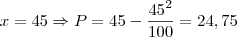
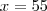 :
: