 por DanielRJ » Dom Dez 18, 2011 13:22
por DanielRJ » Dom Dez 18, 2011 13:22
Olá depois de muito tempo to de volta.
To com duvida nesta questão fiquei nela na prova da Pm-Es:
Luana desenhou em seu caderno o triangulo ABC, cujas medidas B=70º e A=40º o lado BC mede 12,8. A área oupada por esse triangulo é de aproximadamente :
Dados : sen40º=0,64 ; cos40º=0,76; sen70º=0,94 ; cos70º=0,34.Resposta : 120 cm²
Minha resolução:
Usando a lei dos senos temos:
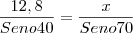
Aqui eu achei os lados :
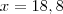
Agora no calculo da area que estou me enrolando!
- Anexos
-

- Questão80.jpg (10.3 KiB) Exibido 1776 vezes
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielRJ » Dom Dez 18, 2011 15:33
por DanielRJ » Dom Dez 18, 2011 15:33
Amigos consegui resolver a questão . Foi muita falta de atenção peço desculpas
Mas a Questão fica ai pra tirar a duvida de alguem:
Resolução :
Sendo : h = 18,8 e b= 12,8
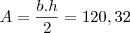
cm

-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações Métricas
por janderson77 » Seg Dez 02, 2013 12:28
- 0 Respostas
- 939 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:28
Geometria Plana
-
- Demonstração Relações Métricas
 por PedroSantos » Ter Dez 07, 2010 22:59
por PedroSantos » Ter Dez 07, 2010 22:59
- 1 Respostas
- 1758 Exibições
- Última mensagem por VtinxD

Dom Dez 12, 2010 22:23
Trigonometria
-
- relaçoes metricas nos triangulos
por stanley tiago » Sáb Fev 12, 2011 19:34
- 4 Respostas
- 2822 Exibições
- Última mensagem por stanley tiago

Dom Fev 13, 2011 18:04
Geometria Plana
-
- relaçoes metricas na circuferencia
 por stanley tiago » Seg Abr 11, 2011 18:37
por stanley tiago » Seg Abr 11, 2011 18:37
- 2 Respostas
- 1996 Exibições
- Última mensagem por stanley tiago

Ter Abr 12, 2011 10:06
Geometria Analítica
-
- Circunferencia e relações metricas
 por alfabeta » Qua Fev 29, 2012 00:09
por alfabeta » Qua Fev 29, 2012 00:09
- 0 Respostas
- 1686 Exibições
- Última mensagem por alfabeta

Qua Fev 29, 2012 00:09
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
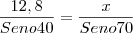
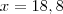


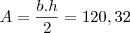 cm
cm
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.