primeira dica:
antes de qualquer coisa isole o y em abas as equações e plote os graficos com algum programa ou na mão mesmo, bem esboçando!... imagine que voce vai girar justamente a parte que está entre as duas! e pense que essa pode ser obtida pela subtração da rotação da menor pela maior.
tente perceber qual das curvas está "por cima". depois, descubra o volume dos solidos da rotação de cada uma das curvas individualmente e subtraia a menor da maior!
se isso ja tiver ajudado tente fazer o exercicio.
Segunda dica: caso isso não tenha ajudado. vamos com mais calma:
temos as duas curvas

e
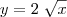

Uploaded with
ImageShack.usessas curvas se encontram em dois pontos.
Esses dois pontos são os que delimitam os limites de integração. pois afinal estaremos efetuando a rotação só entre eles.
resolvendo a equação
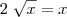
voce obtém

e

faça a rotação entre esses dois ptos da função
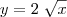
e subtraia desse resultado a rotação da função y = x entre os mesmos ptos!
 e
e 

 e
e 


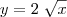

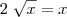
 e
e 
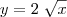

e

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)