 por joaofonseca » Sáb Dez 03, 2011 19:40
por joaofonseca » Sáb Dez 03, 2011 19:40
Esta é uma questão de um exame nacional de Matematica em Portugal.
Eu consegui encontrar a resposta graficamente:
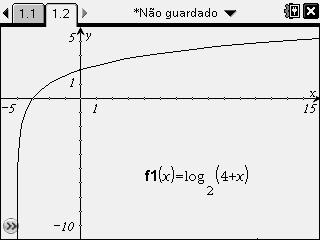
- questao.jpg (10.67 KiB) Exibido 2148 vezes
Como se pode ver quando

,
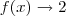
.
Mas não consegui resolver analiticamente.Não consegui resolver a parte:
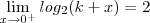
Como é posivel resolver a equação logaritmica dentro do limite?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por joaofonseca » Sáb Dez 03, 2011 21:07
por joaofonseca » Sáb Dez 03, 2011 21:07
Então podemos afirmar que:
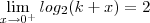
e
![log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2 log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2](/latexrender/pictures/cbc50454fee1189f4a7adbd9aa1f5774.png)
são a mesma coisa?!?
Na segunda expressão, primeiro calcula-se o limite e depois resolve-se a equação logaritmica.
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sáb Dez 03, 2011 21:27
por LuizAquino » Sáb Dez 03, 2011 21:27
joaofonseca escreveu:Então podemos afirmar que:
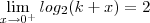
e
![log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2 log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2](/latexrender/pictures/cbc50454fee1189f4a7adbd9aa1f5774.png)
são a mesma coisa?!?
De modo geral, é verdadeira a seguinte afirmação:
Se
f é contínua em
L e

, então
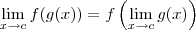
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,
,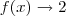 .
.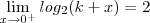


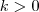 , você pode resolver o limite diretamente:
, você pode resolver o limite diretamente:

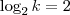
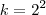


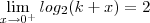
![log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2 log_{2} \left[ \lim_{x \to 0^+}(k+x) \right]=2](/latexrender/pictures/cbc50454fee1189f4a7adbd9aa1f5774.png)
 , então
, então 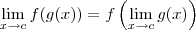 .
.