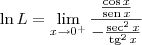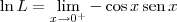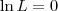por Thamc » Sex Dez 02, 2011 19:26
por Thamc » Sex Dez 02, 2011 19:26
Tenho um exercício de cálculo que sempre chego na mesma resposta, mas acho que errei algo no meio e está errado.
(sei que é produto indeterminado, mas não o tipo)
por L'hospital:

Me perco no meio!
-
Thamc
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Dez 02, 2011 19:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Geofísica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida]Função Trigonométrica Inversa em Integral.
por Jhonata » Qui Jun 07, 2012 18:06
- 2 Respostas
- 1943 Exibições
- Última mensagem por Jhonata

Qui Jun 07, 2012 20:40
Cálculo: Limites, Derivadas e Integrais
-
- [Função composta]Achar o dominio de uma função composta
por lucasmath » Dom Abr 12, 2015 16:09
- 0 Respostas
- 2229 Exibições
- Última mensagem por lucasmath

Dom Abr 12, 2015 16:09
Funções
-
- Duvida com L'Hospital
por Gustavooguto » Qua Nov 12, 2014 09:30
- 1 Respostas
- 2097 Exibições
- Última mensagem por adauto martins

Qua Nov 12, 2014 12:25
Cálculo: Limites, Derivadas e Integrais
-
- [FUNÇÃO] NAO CONSIGO ENTENDER FUNÇÃO COMPOSTA!
por Gabriela AlmeidaS » Seg Mai 12, 2014 19:18
- 5 Respostas
- 5452 Exibições
- Última mensagem por Toussantt

Dom Jan 24, 2016 15:34
Funções
-
- [Duvida] Derivada da Composta
por demolot » Qua Mai 25, 2011 13:04
- 4 Respostas
- 2075 Exibições
- Última mensagem por demolot

Qui Mai 26, 2011 12:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






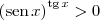 quando
quando 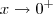 , temos que deve ocorrer
, temos que deve ocorrer  . Vamos fazer a suposição de que L seja não nulo, isto é, que temos apenas
. Vamos fazer a suposição de que L seja não nulo, isto é, que temos apenas  . Desse modo, podemos aplicar o logaritmo natural em ambos os membros da equação acima:
. Desse modo, podemos aplicar o logaritmo natural em ambos os membros da equação acima:![\ln L = \ln \left[\lim_{x\to 0^+} \left(\textrm{sen}\, x\right)^{\textrm{tg}\, x}\right] \ln L = \ln \left[\lim_{x\to 0^+} \left(\textrm{sen}\, x\right)^{\textrm{tg}\, x}\right]](/latexrender/pictures/040d1094e32ac249a461c45ea3999f9d.png)
![\ln L = \lim_{x\to 0^+} \ln \left[\left(\textrm{sen}\, x\right)^{\textrm{tg}\, x}\right] \ln L = \lim_{x\to 0^+} \ln \left[\left(\textrm{sen}\, x\right)^{\textrm{tg}\, x}\right]](/latexrender/pictures/5a1da8646623abd46d181a5916b8a4eb.png)


![\ln L = \lim_{x\to 0^+} \frac{\left[\ln \left(\textrm{sen}\, x\right)\right]^\prime}{\left(\frac{1}{\textrm{tg}\, x}\right)^\prime} \ln L = \lim_{x\to 0^+} \frac{\left[\ln \left(\textrm{sen}\, x\right)\right]^\prime}{\left(\frac{1}{\textrm{tg}\, x}\right)^\prime}](/latexrender/pictures/e74c4e853557adac2d43640504f36e46.png)