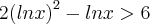
Resposta:
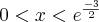 ou
ou 
Agradeço quem resolver!

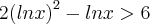
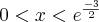 ou
ou 

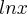 .
.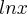 = u , teremos:
= u , teremos: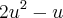 maior que 6
maior que 6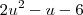 maior que 0
maior que 0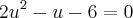
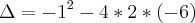



 menor que
menor que  ou
ou  maior que
maior que 
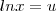 .
.
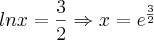
 maior que 0
maior que 0 menor que
menor que 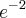
 maior que
maior que 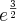
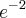 ou
ou  maior que
maior que 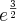

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes