


bernardo1744 escreveu:boa tarde pessoal. eu queria muito tirar uma dúvida sobre uma questão de prova . na minha prova foi dada a seguinte função [CÁLCULO 1] ache F(x)= e^(x^2-1) , e estava pedindo pra achar as assíntotas , os pontos críticos e os pontos de inflexão. me ajudem por favor. desde já grato ^^



bernardo1744 escreveu:minha dúvida é q eu não sei achar assintota em função desse tipo e a do ponto de inflexão eu queria ver qnto que dava sabe
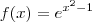 não tem assíntotas. Para uma explicação sobre assíntotas, vide o tópico:
não tem assíntotas. Para uma explicação sobre assíntotas, vide o tópico: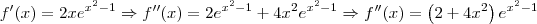
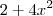 quanto o termo
quanto o termo 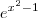 são sempre positivos e não nulos. Portanto, temos que
são sempre positivos e não nulos. Portanto, temos que 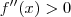 para todo x no domínio de
para todo x no domínio de 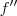 . Logo, o gráfico de f não tem ponto de inflexão e sua concavidade é sempre para cima.
. Logo, o gráfico de f não tem ponto de inflexão e sua concavidade é sempre para cima.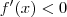 (ou seja, f decresce no intervalo
(ou seja, f decresce no intervalo 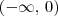 ).
).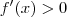 (ou seja, f cresce no intervalo
(ou seja, f cresce no intervalo  ).
).
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes