Um arame de 4 metros de comprimento é cortado em dois pedaços, sendo um dobrado em
forma de quadrado e outro em forma de círculo (o arame será colocado como perímetro destas
figuras)
Se um pedaço x for usado para formar o quadrado, então temos que um pedaço 4-x será usado para formar o círculo.
Como devemos cortar o arame para que as somas das áreas englobadas pelos dois
pedaços seja:
a) Máxima?
b) Mínima?
Sabemos que se L é o lado de um quadrado, então o seu perímetro vale 4L. Sendo assim, temos que:
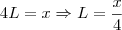
Por outro lado, sabemos que se R é o raio de uma circunferência, então o seu comprimento vale
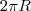
. Sendo assim, temos que:

A soma das áreas, dependendo do valor x, será dada por
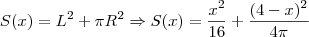
Considere que o domínio de S seja D = [0, 4]. Nesse caso, x = 0 significa que fizemos apenas um círculo com o arame. Por outro lado, x = 4 significa que fizemos apenas um quadrado com o arame. Em ambos os casos, nós "dividimos" o arame em dois pedaços: um pedaço com comprimento 0; um pedaço com comprimento 4.
Agora, para achar o máximo ou o mínimo de
f, utilize o
Método do Intervalo Fechado:
- determine os pontos críticos de f. Isto é, os pontos x = c tais que
 ou
ou  não existe;
não existe; - calcule o valor de f nos seus pontos críticos. Isto é, calcule f(c);
- calcule o valor de f em 0 e em 4; Isto é, calcule f(0) e f(4);
- o menor dos valores calculados nos passos 2 e 3 será o mínimo global. Já o maior dos valores será o máximo global.


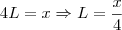
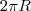 . Sendo assim, temos que:
. Sendo assim, temos que:
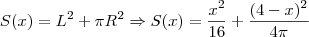
 ou
ou  não existe;
não existe;

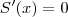 , você irá obter que só há um ponto crítico:
, você irá obter que só há um ponto crítico:  .
.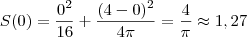

![S\left(\frac{16}{\pi+4}\right) = \frac{\left(\frac{16}{\pi+4}\right)^2}{16} + \frac{\left[4-\left(\frac{16}{\pi+4}\right)\right]^2}{4\pi} = \frac{4}{4+\pi}\approx 0,56 S\left(\frac{16}{\pi+4}\right) = \frac{\left(\frac{16}{\pi+4}\right)^2}{16} + \frac{\left[4-\left(\frac{16}{\pi+4}\right)\right]^2}{4\pi} = \frac{4}{4+\pi}\approx 0,56](/latexrender/pictures/13cb4d6813bc1728a07a4d56ce20a432.png)
 .
.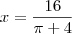 . Isso significa que temos um quadrado de lado
. Isso significa que temos um quadrado de lado  e um círculo de raio
e um círculo de raio  .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.