 por cal12 » Dom Nov 27, 2011 16:46
por cal12 » Dom Nov 27, 2011 16:46
a) A equação do movimento de uma partícula é
![s(t)=\sqrt[3]{t+2} s(t)=\sqrt[3]{t+2}](/latexrender/pictures/034fb281ed6be2f36c01dda9e28b8d51.png)
, s em metros, t em segundos. Determine:
a1) o instante em que a velocidade é de 1/12 m/s.
a2) a distância percorrida até esse instante.
a3) a aceleração da partícula quando t = 2 seg.
estava estudando pela internet taxa de variacao mas quando vou responder, as respostas nao batem com a que me foi informado e gostaria que me esplicasse como fazer o exercicio.
Editado pela última vez por
cal12 em Seg Nov 28, 2011 09:27, em um total de 1 vez.
-
cal12
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Ago 14, 2011 11:21
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por LuizAquino » Dom Nov 27, 2011 19:21
por LuizAquino » Dom Nov 27, 2011 19:21
Quais foram as suas tentativas?
Por favor, indique exatamente onde está a sua dúvida.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por andersoneng » Sex Jun 29, 2012 10:46
por andersoneng » Sex Jun 29, 2012 10:46
tambem tenho duvidas em relacao a essa questao !
as minhas resposta dao
a) 6,8. resposta do gabarito - 6
essa primeira resposta implica em todas as outras ! meu professor me deu meio certo nessa questao !!
-
andersoneng
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Jun 25, 2012 20:46
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Graduação Engenharia de Produção
- Andamento: cursando
 por Russman » Sex Jun 29, 2012 22:01
por Russman » Sex Jun 29, 2012 22:01
Veja que a velocidade da partícula é dada por
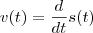
,
o distância percorrida entre os instantes
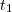
e

por
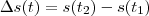
,
e a aceleração por
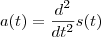
.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Taxa de variação
por felipe_ad » Ter Jun 29, 2010 19:44
- 2 Respostas
- 60600 Exibições
- Última mensagem por Guill

Ter Fev 21, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de variação
 por AlbertoAM » Sáb Mai 21, 2011 14:23
por AlbertoAM » Sáb Mai 21, 2011 14:23
- 1 Respostas
- 5488 Exibições
- Última mensagem por LuizAquino

Dom Mai 22, 2011 13:03
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por AlbertoAM » Sáb Mai 28, 2011 15:53
por AlbertoAM » Sáb Mai 28, 2011 15:53
- 10 Respostas
- 10622 Exibições
- Última mensagem por AlbertoAM

Ter Mai 31, 2011 21:32
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por Pollyanna Moraes » Sáb Out 22, 2011 17:37
por Pollyanna Moraes » Sáb Out 22, 2011 17:37
- 1 Respostas
- 8458 Exibições
- Última mensagem por LuizAquino

Dom Out 23, 2011 10:15
Cálculo: Limites, Derivadas e Integrais
-
- taxa de variaçao
por matmatco » Dom Abr 29, 2012 20:26
- 3 Respostas
- 10919 Exibições
- Última mensagem por Guill

Ter Mai 01, 2012 13:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![s(t)=\sqrt[3]{t+2} s(t)=\sqrt[3]{t+2}](/latexrender/pictures/034fb281ed6be2f36c01dda9e28b8d51.png) , s em metros, t em segundos. Determine:
, s em metros, t em segundos. Determine:


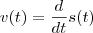 ,
,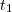 e
e  por
por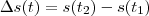 ,
,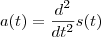 .
.