 por Beatriz4 » Sex Nov 25, 2011 23:45
por Beatriz4 » Sex Nov 25, 2011 23:45
Já resolvi este limite mas não me dá o valor certo. Vou colocar aqui a minha resolução e gostaria que alguém me dissesse onde está o meu erro(s).
(n->+inf)lim (2^(2n+1))*((n+2)/(4n+1))^n
lim (2^(2n+1))*((n+2)/(4n+1))^n = lim ((2^(2n+1))/((n+2)/(4n+1))^n)*(((n+2)/(4n+1))^n)/((n+2)/(4n+1))^n = lim 2*((2^2)^n)/((n+2)/(4n+1))^n =
= lim 2*(4/((n+2)/(4n+1)))^n = lim 2*(4(4n+1)/(n+2)))^n = lim 2 ((16n+4)/(n+2))^n
Até aqui penso estar bem, gostaria que me dissessem como continuar para saber se a minha resoluçã está correcta. segundo um progrma de resolução de limites este dá 2e^(7/4) e a mim deu-me +inf.
Agradecia mesmo se me ajudassem!
-
Beatriz4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Nov 25, 2011 21:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Biomédica
- Andamento: cursando
 por Beatriz4 » Dom Nov 27, 2011 11:05
por Beatriz4 » Dom Nov 27, 2011 11:05
Obrigada pela ajuda =)
-
Beatriz4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Nov 25, 2011 21:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Biomédica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5409 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4755 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4782 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4808 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2793 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


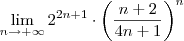

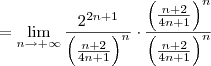
![= \lim_{n\to +\infty} 2\cdot \frac{\left[\left(2^2\right)^n\right]}{\left(\frac{n+2}{4n+1}\right)^n} = \lim_{n\to +\infty} 2\cdot \frac{\left[\left(2^2\right)^n\right]}{\left(\frac{n+2}{4n+1}\right)^n}](/latexrender/pictures/d339d548cb0f1bfefe349f62761166f2.png)
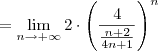
![= \lim_{n\to +\infty} 2\cdot \left[\frac{4(4n+1)}{n+2}\right]^n = \lim_{n\to +\infty} 2\cdot \left[\frac{4(4n+1)}{n+2}\right]^n](/latexrender/pictures/34c572e1fcf721d110e6f8ab07168d46.png)

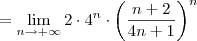
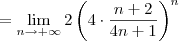
![= \lim_{n\to +\infty} 2\left[4 \cdot \frac{n\left(1+\frac{2}{n}\right)}{4n\left(1+\frac{1}{4n}\right)}\right]^n = \lim_{n\to +\infty} 2\left[4 \cdot \frac{n\left(1+\frac{2}{n}\right)}{4n\left(1+\frac{1}{4n}\right)}\right]^n](/latexrender/pictures/96db24173607db5a1736936edc5d6bc5.png)
![= \lim_{n\to +\infty} 2\left[\frac{\left(1+\frac{2}{n}\right)}{\left(1+\frac{1}{4n}\right)}\right]^n = \lim_{n\to +\infty} 2\left[\frac{\left(1+\frac{2}{n}\right)}{\left(1+\frac{1}{4n}\right)}\right]^n](/latexrender/pictures/a9e35f0a42159ad0208f3536830c4754.png)
![= 2\left[\frac{\displaystyle{\lim_{n\to +\infty}\left(1+\frac{2}{n}\right)^n}}{\displaystyle{\lim_{n\to +\infty} \left(1+\frac{1}{4n}\right)^n}}\right] = 2\left[\frac{\displaystyle{\lim_{n\to +\infty}\left(1+\frac{2}{n}\right)^n}}{\displaystyle{\lim_{n\to +\infty} \left(1+\frac{1}{4n}\right)^n}}\right]](/latexrender/pictures/bd6072b191231b432d001cce14a2ec91.png)
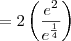

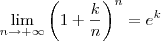
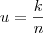 , temos que:
, temos que:
![= \lim_{u\to 0} \left[\left(1+u\right)^\frac{1}{u}\right]^k = \lim_{u\to 0} \left[\left(1+u\right)^\frac{1}{u}\right]^k](/latexrender/pictures/afa9f6fb4c197955adf4eabbe8cfed11.png)
![= \left[\lim_{u\to 0} \left(1+u\right)^\frac{1}{u}\right]^k = \left[\lim_{u\to 0} \left(1+u\right)^\frac{1}{u}\right]^k](/latexrender/pictures/affc204aaf4f29f3420cd051859bf336.png)



 .
.



