 por Aliocha Karamazov » Sáb Nov 26, 2011 18:40
por Aliocha Karamazov » Sáb Nov 26, 2011 18:40
Pessoal, o problema é esse:
Dois carros iniciam o movimento no mesmo ponto. Um viaja para o sul a 60km/h e o outro para oeste a 25km/h. A que taxa esta crescendo a distância entre os carros duas horas a depois?
Esse parece ser um problema realmente fácil, mas eu não entendo muito bem o que se pede.
Bem, a taxa com que cresce a distância é a derivada do espaço em relação ao tempo. De acordo com o exercício, temos dois vetores-velocidade perpendiculares. A taxa com que cresce a distância entre os dois carros, no meu entender, é a velocidade relativa entre eles. Como os vetores são perpendiculares, podemos utilizar o Teorema de Pitágoras para calcular a velocidade relativa.
Como as velocidades são constantes, esse vetor velocidade relativa também seria constante. Mas deve haver algo muito errado na minha interpretação. Caso contrário, o exercício não pederia a "taxa com que está crescendo a distância entre os carros duas horas a depois".
Gostaria que alguém me ajudasse na interpretação do problema e apontasse "um vetor" para guiar minha solução...
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Sáb Nov 26, 2011 19:01
por LuizAquino » Sáb Nov 26, 2011 19:01
Aliocha Karamazov escreveu:Dois carros iniciam o movimento no mesmo ponto. Um viaja para o sul a 60km/h e o outro para oeste a 25km/h. A que taxa esta crescendo a distância entre os carros duas horas a depois?
Aliocha Karamazov escreveu:Esse parece ser um problema realmente fácil, mas eu não entendo muito bem o que se pede.
(...)
Gostaria que alguém me ajudasse na interpretação do problema e apontasse "um vetor" para guiar minha solução...
Vide o tópico abaixo para ter uma ideia:
isntante (t) derivadaviewtopic.php?f=120&t=6242
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Aliocha Karamazov » Sáb Nov 26, 2011 19:15
por Aliocha Karamazov » Sáb Nov 26, 2011 19:15
Tomando
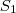
e

como a posição no espaço de cada carro, a distância entre eles é

.
Onde

e

Assim,

Temos que

Ou seja, a taxa de variação é constante. É isso mesmo? O exercício não pode ser apenas isso...
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por MarceloFantini » Dom Nov 27, 2011 01:57
por MarceloFantini » Dom Nov 27, 2011 01:57
Porque não? A velocidade de ambos é constante, não há aceleração.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Taxa de Variação
por Vanny » Dom Set 30, 2012 20:58
- 0 Respostas
- 3110 Exibições
- Última mensagem por Vanny

Dom Set 30, 2012 20:58
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] - Taxa de Variação
por Jeks_Osodrac » Ter Jul 30, 2013 19:19
- 3 Respostas
- 3269 Exibições
- Última mensagem por Russman

Qua Jul 31, 2013 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivada como Taxa de Variação
por Ronaldobb » Sex Set 21, 2012 20:29
- 3 Respostas
- 2264 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 00:05
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Taxa de variação - velocidade
por emanes » Qua Out 17, 2012 11:10
- 1 Respostas
- 3929 Exibições
- Última mensagem por young_jedi

Qua Out 17, 2012 11:50
Cálculo: Limites, Derivadas e Integrais
-
- Derivada taxa de variação - HELP Por favor
por vivik » Ter Mai 15, 2018 16:47
- 0 Respostas
- 2956 Exibições
- Última mensagem por vivik

Ter Mai 15, 2018 16:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



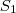 e
e  como a posição no espaço de cada carro, a distância entre eles é
como a posição no espaço de cada carro, a distância entre eles é  .
. e
e 



