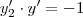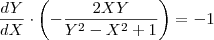manolo223 escreveu:Encontre a família de curvas ortogonais a família de círculos que contém os pontos (1,0) e (-1,0).
manolo223 escreveu:Como eu montaria a equaçao para resolver la? meu problema esta na interpretaçao para montar a equaçao.
Primeiro, determine a família de circunferências (e não de círculos como diz o exercício) que contém os pontos (1,0) e (-1,0).
Lembre-se que a equação de uma circunferência de centro (xc, yc) e raio r é dada por:
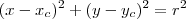
Substituindo os pontos dados, você obtém o sistema:

A solução desse sistema é

e
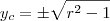
.
Temos então duas famílias de circunferências:
(i)
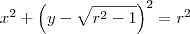
;
(ii)

.
Vamos considerar primeiro a família (i).
Derivando implicitamente, temos que:

Precisamos agora eliminar da expressão da derivada o termo

, para que a derivada fique em função apenas de x e y. Para isso, vamos usar a equação da circunferência:

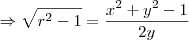
Desse modo, podemos escrever que:
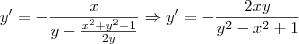
Para que uma outra curva
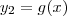
seja ortogonal a essa família de circunferências, em todos os pontos de interseção (X, Y) entre essas curvas devemos ter:
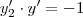
Ou seja, precisamos resolver a EDO:
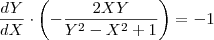
Agora tente terminar o exercício.
Vale lembrar que depois você deve seguir esse mesmo raciocínio para a família de circunferências (ii).


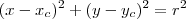

 e
e 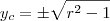 .
.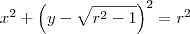 ;
; .
.
 , para que a derivada fique em função apenas de x e y. Para isso, vamos usar a equação da circunferência:
, para que a derivada fique em função apenas de x e y. Para isso, vamos usar a equação da circunferência:
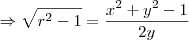
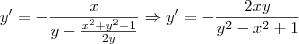
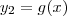 seja ortogonal a essa família de circunferências, em todos os pontos de interseção (X, Y) entre essas curvas devemos ter:
seja ortogonal a essa família de circunferências, em todos os pontos de interseção (X, Y) entre essas curvas devemos ter: