 por rhodry » Ter Nov 22, 2011 17:49
por rhodry » Ter Nov 22, 2011 17:49
olá pessoal se possível alguém demonstrar está situação, agradeço, não estou conseguindo raciocinar...
2. O senhor Jurandir é dono de um pequeno terreno quadrado de 36m de lado. Ele pretende colocar uma irrigação na sua plantação de feijão. Para isso escolheu um modelo que joga água em forma circular a partir de um ponto central.
a) A primeira ideia foi usar um único dispersor para irrigação localizado no centro de seu terreno, como na figura ao lado. Qual será a área irrigada por esse dispersor? Explique seu raciocínio e não use aproximações para

.
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por rhodry » Ter Nov 22, 2011 17:59
por rhodry » Ter Nov 22, 2011 17:59
Preciso resolver esta situação, mas não estou conseguindo, pensei em determinar o raio, fico me perguntando donde poderei relacionar os valores fornecidos, para chegar em uma conclusão.
2. O senhor Jurandir é dono de um pequeno terreno quadrado de 36m de lado. Ele pretende colocar uma irrigação na sua plantação de feijão. Para isso escolheu um modelo que joga água em forma circular a partir de um ponto central.
b) Outra opção seria usar 4 dispersores idênticos, mas de menor alcance do que o dispersor usado na primeira ideia, dispostos como na figura ao lado. Qual será a área irrigada por eles? Explique seu raciocínio e não use aproximações para

.
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por lucinei daliberto » Qua Nov 23, 2011 18:54
por lucinei daliberto » Qua Nov 23, 2011 18:54
rhodry escreveu:olá pessoal se possível alguém demonstrar está situação, agradeço, não estou conseguindo raciocinar...
2. O senhor Jurandir é dono de um pequeno terreno quadrado de 36m de lado. Ele pretende colocar uma irrigação na sua plantação de feijão. Para isso escolheu um modelo que joga água em forma circular a partir de um ponto central.
a) A primeira ideia foi usar um único dispersor para irrigação localizado no centro de seu terreno, como na figura ao lado. Qual será a área irrigada por esse dispersor? Explique seu raciocínio e não use aproximações para

.
evoce faz parte da Redefor? porque estou com o mesmo problema ja não sei onde procurar,
-
lucinei daliberto
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qua Out 26, 2011 16:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por MarceloFantini » Qua Nov 23, 2011 19:10
por MarceloFantini » Qua Nov 23, 2011 19:10
E as figuras?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rhodry » Qui Nov 24, 2011 19:37
por rhodry » Qui Nov 24, 2011 19:37
Olá Lucinei, sim faço parte do redefor, e as vezes tem conteúdo complicado, por acaso tiver interesse em compartilhar situações, o meu e-mail
rhodry_jr@hotmail.com
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por rhodry » Qui Nov 24, 2011 19:50
por rhodry » Qui Nov 24, 2011 19:50
olá marcelo, tudo bem... as imagems se encontram no seguinte link.
http://imageshack.us/photo/my-images/82 ... 00107.jpg/ por acaso puder me ajudar fico grato, tive o seguinte raciocinio,
Se a área do quadrado tem 36m, e a circunferencia ocupa todas as do quadrado no ponto médio de cada lado.
Então o raio será 18.
No entanto para calcular a área de um circunferência temos:
Ac=


A=

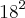
A=

324m
portanto a área será de 324

m
mas não sei se meu raciocínio esta´certo... se puder dar uma olhado,, ficarei agradecido.
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Nov 24, 2011 21:08
por MarceloFantini » Qui Nov 24, 2011 21:08
Está certo. Faça analogamente para os outros.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rhodry » Sex Nov 25, 2011 19:49
por rhodry » Sex Nov 25, 2011 19:49
Fiz para os demais situações, mas cheguei ao mesmo resultado iguais para todos,,, ser´que estou correto?
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sex Nov 25, 2011 20:49
por MarceloFantini » Sex Nov 25, 2011 20:49
Sim. Note que para o caso em que ao invés de uma temos quatro circunferências cujos raios são a metade do original, temos que para a área de uma delas:
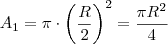
. Mas a área total coberta por todas é quatro vezes a área de uma, logo
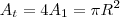
, que é igual a área original.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.





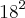
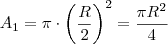 . Mas a área total coberta por todas é quatro vezes a área de uma, logo
. Mas a área total coberta por todas é quatro vezes a área de uma, logo 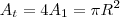 , que é igual a área original.
, que é igual a área original. } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: