
Este exercício eu não sei nem como começar.
Desde já agradeço!!!



Andreza escreveu:Qual é o volume de um sólido gerado pela rotação de um triângulo equilátero de lado x, ao redor de um de seus lados?
Andreza escreveu:Este exercício eu não sei nem como começar.

![\Pix{r}^{3}\sqrt[]{3}/3 \Pix{r}^{3}\sqrt[]{3}/3](/latexrender/pictures/16718e51b019bcc87c22efc3a6dc5e1c.png) mas não tem o l pra mim substituir o lado do triangulo q é x. Qual outra fórmula eu uso?
mas não tem o l pra mim substituir o lado do triangulo q é x. Qual outra fórmula eu uso?


Andreza escreveu:Pra mim achar o volume de um sólido gerado pela rotação de um triangulo equilatero de lado x, ao redor de um de seus lados eu pesquisei a fórmula do volume do cone q émas não tem o l pra mim substituir o lado do triangulo q é x. Qual outra fórmula eu uso?

 , onde o raio da base r é correspondente a metade do lado do triângulo equilátero.
, onde o raio da base r é correspondente a metade do lado do triângulo equilátero.Andreza escreveu:Mesmo com a figura não conseguir resolvê-lo.
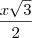 (que corresponde a altura h do triângulo equilátero de lado x).
(que corresponde a altura h do triângulo equilátero de lado x). .
.

Andreza escreveu:Colocando na fórmula substituindo r por x raiz de 3 dividido por 2 eu encontrei o volume de um cone igual a 3pi x elevado a terceira dividido por 8. Multiplicando o resultado por 2 = 3pi x elevado a terceira dividido por 4. Está correto?

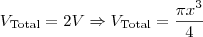


Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

