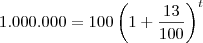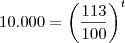gedeaocosta escreveu:Juca juntou alguns meses de sua mesada perfazendo um total de R$ 100,00. (...)
O capital C do Juca:
C = 100
gedeaocosta escreveu:(...) Feliz, perguntou a seu pai em quanto tempo obteria um milhão de reais se aplicasse seu dinheiro. (...)
O montante M que Juca deseja:
M = 1.000.000
gedeaocosta escreveu:(...) Sereno, seu pai afirmou: – Filho, mesmo que você aplique seu capital a juros compostos a uma taxa de 13% ao ano, capitalizados anualmente, talvez não esteja vivo quando alcançar seu milhão. (...)
A aplicação será de juros compostos, com taxa anual de 13%. Chamando i de taxa, temos i=13% (ou seja,
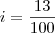
).
gedeaocosta escreveu:(...) Neste contexto, considerando que os cálculos de seu pai estejam certos, o número mínimo de
anos de que Juca necessitaria para conseguir o montante de seu sonho está compreendido
entre (adote
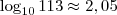
): (...)
Sabemos que o montante M obtido pela aplicação do capital C, em regime de juros compostos com taxa i e tempo t, é dado por:

Usando as informações do exercício, deseja-se calcular t (em anos) tal que:
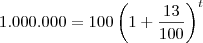
Comece a solução dividindo ambos os membros da equação por 100:

Efetue a soma que aparece dentro dos parênteses:
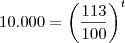
Em seguida, aplique o logaritmo na base 10 em ambos os membros da equação:

Agora tente usar as propriedades dos logaritmos para terminar o exercício.
ObservaçãoPara revisar o conteúdo sobre juros compostos, eu recomendo que você leia a página:
Juros Compostos - Brasil Escolahttp://www.brasilescola.com/matematica/ ... postos.htm

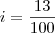 ).
).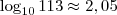 ): (...)
): (...)