Ana_Rodrigues escreveu:Obter uma equação da parábola que satisfaça as condições dadas
vértice: V(4,-3); eixo dos x, passando pelo ponto P(2,1)
Eu vou assumir que a condição "eixo dos x" significa que o eixo de simetria da parábola deve ser paralelo ao eixo x. Se não for isso, então por favor informe o que significa "eixo dos x" no livro (ou material) de onde você retirou essa questão.
Assumindo essa condição, note que a concavidade dessa parábola é para a esquerda (já que a coordenada x de P é menor do que a coordenada x de V).
Sendo assim, a equação dessa parábola tem o formato:

, sendo (h, k) o vértice da parábola e p a distância entre o foco e a diretriz.
Já que V=(4, -3), então temos que h = 4 e k = -3. Portanto a equação fica:
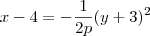
Já que a parábola deve passar pelo ponto P=(2, 1), substituindo x = 2 e y = 1 na equação da parábola, ficamos com:

Resolvendo essa equação você obtém que p = 4.
Portanto, a equação da parábola será:
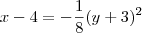


 , sendo (h, k) o vértice da parábola e p a distância entre o foco e a diretriz.
, sendo (h, k) o vértice da parábola e p a distância entre o foco e a diretriz.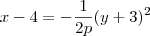

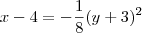



 , avisa que eu resolvo.
, avisa que eu resolvo.

