 por anne leticia » Sex Nov 18, 2011 20:48
por anne leticia » Sex Nov 18, 2011 20:48
Bom gente a questão que estou com dúvidas é essa que esta ai embaixo,ja tentei resolvê-la de diversas formas,mas nada deu certo .
Na alternativa 'a' eu fiz este calculo : a²=4xPIxr²
a²=4xPIX(12)²
a²=4PIx(144)
a²= 576
a²= raiz quadrada de 576 = 24
Já a alternativa 'b' ... = c=r²
c=676 ²
c= raiz quadrada de 676 que dá 26 !
Embora eu tenha certeza que esses cálculos que fiz acima não estao de acordo com o que a questao pede sendo assim não estão corretos .
Uma esfera cuja superficie tem area igual a 676 pi cm² é cortada por um plano situado a uma distancia de 12 cm do seu centro, determinando um circulo. Nessas condições, determine:
a] A area desse circulo
b] O comprimento da circunferencia maxima dessa esfera
c] O volume do cone reto cujo vertice é o centro da esfera e a base é o circulo determinado pela intersecçao do plano com a esfera.
-
anne leticia
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 18, 2011 20:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sex Nov 18, 2011 22:38
por MarceloFantini » Sex Nov 18, 2011 22:38
A área da esfera é dada por

cm. O plano é paralelo à circunferência equatorial, e portanto podemos formar um triângulo retângulo traçando o raio até o círculo, onde teremos a hipotenusa sendo o raio da esfera, a altura sendo a distância do centro do círculo até o centro da esfera e o outro cateto o raio do círculo. Aplicando pitágoras, encontramos

cm. Daí, a área do círculo é
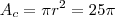

.
O comprimento da circunferência máxima é simplesmente

cm.
O volume do cone será
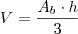
onde a área da base é a área do círculo e a altura a distância entre os centros, logo

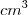
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por anne leticia » Sáb Nov 19, 2011 10:23
por anne leticia » Sáb Nov 19, 2011 10:23
OBRIGADA ! Me ajudou bastante !Beijos
-
anne leticia
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 18, 2011 20:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Me ajudem nessa questão de Geometria Espacial
por ariana » Sáb Set 12, 2009 18:24
- 5 Respostas
- 4545 Exibições
- Última mensagem por Elcioschin

Dom Set 13, 2009 20:55
Geometria Espacial
-
- [porcentagem] Ajudem nessa questão?
por amanda s » Sex Nov 15, 2013 20:20
- 2 Respostas
- 3508 Exibições
- Última mensagem por nakagumahissao

Sáb Nov 16, 2013 01:04
Conversão de Unidades
-
- [logica] Ajudem nessa questão
por amanda s » Sáb Nov 16, 2013 09:56
- 1 Respostas
- 1607 Exibições
- Última mensagem por nakagumahissao

Sáb Nov 16, 2013 14:56
Lógica
-
- [probabilidade] ajudem nessa questão
por amanda s » Sáb Nov 16, 2013 12:33
- 1 Respostas
- 1584 Exibições
- Última mensagem por nakagumahissao

Sáb Nov 16, 2013 14:56
Probabilidade
-
- [porcentagem] Ajudem nessa questão?
por amanda s » Sáb Nov 16, 2013 17:24
- 0 Respostas
- 2233 Exibições
- Última mensagem por amanda s

Sáb Nov 16, 2013 17:24
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 cm. O plano é paralelo à circunferência equatorial, e portanto podemos formar um triângulo retângulo traçando o raio até o círculo, onde teremos a hipotenusa sendo o raio da esfera, a altura sendo a distância do centro do círculo até o centro da esfera e o outro cateto o raio do círculo. Aplicando pitágoras, encontramos
cm. O plano é paralelo à circunferência equatorial, e portanto podemos formar um triângulo retângulo traçando o raio até o círculo, onde teremos a hipotenusa sendo o raio da esfera, a altura sendo a distância do centro do círculo até o centro da esfera e o outro cateto o raio do círculo. Aplicando pitágoras, encontramos  cm. Daí, a área do círculo é
cm. Daí, a área do círculo é 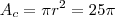
 .
. cm.
cm.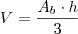 onde a área da base é a área do círculo e a altura a distância entre os centros, logo
onde a área da base é a área do círculo e a altura a distância entre os centros, logo 
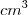 .
.
