 por beel » Sex Nov 18, 2011 14:28
por beel » Sex Nov 18, 2011 14:28
nessa integral
![\int_{1}^{9} (\sqrt[]{t} - \frac{4}{\sqrt[]{t}}) dt \int_{1}^{9} (\sqrt[]{t} - \frac{4}{\sqrt[]{t}}) dt](/latexrender/pictures/173f1fd9324efd4a778dc80c29eb0316.png)
fiquei em duvida com a raiz...tentei transforma-la em potencia fracionária (meio)
e ficou

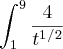
ai preciso achar a primitiva de cada funçao , aplica-las nos extremos ( 9 e 1) e subtrair o resultado ?
...ficaria

aplicado em 9, em 1...depois de subtrair ficou

Na segunda integral, ficaria

Assim o resultado seria 4/3 é isso mesmo?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Sex Nov 18, 2011 16:25
por MarceloFantini » Sex Nov 18, 2011 16:25
Seu método está certo, use este site para conferir numericamente:
www.wolframalpha.com .
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral Definida] Denominador c/ fator x e raiz de binômio
por Matheus Lacombe O » Dom Mar 17, 2013 17:35
- 2 Respostas
- 5907 Exibições
- Última mensagem por Matheus Lacombe O

Qua Mar 20, 2013 13:25
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:29
- 1 Respostas
- 1840 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:05
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:48
- 1 Respostas
- 1983 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:07
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 12:53
- 1 Respostas
- 2017 Exibições
- Última mensagem por LuizAquino

Sex Nov 18, 2011 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida
por beel » Sex Nov 18, 2011 13:29
- 1 Respostas
- 1723 Exibições
- Última mensagem por MarceloFantini

Sex Nov 18, 2011 16:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{1}^{9} (\sqrt[]{t} - \frac{4}{\sqrt[]{t}}) dt \int_{1}^{9} (\sqrt[]{t} - \frac{4}{\sqrt[]{t}}) dt](/latexrender/pictures/173f1fd9324efd4a778dc80c29eb0316.png)

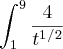
 aplicado em 9, em 1...depois de subtrair ficou
aplicado em 9, em 1...depois de subtrair ficou 




