exercício da redefor vou tentar te orientar resolvendo uma outra raiz
Vou pegar
![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png)
, a primeira coisa é descobrir o resultado da raíz está entre quais números inteiros. evidente que está entre 2 e 3, então escreveremos assim
![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png)
com x > 1
De
![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png)
decorre que:
![\sqrt[]{7}- 2 = \frac{1}{x} \sqrt[]{7}- 2 = \frac{1}{x}](/latexrender/pictures/a2200a1972c4eb175e43e9481711087a.png)
![x = \frac{1}{\sqrt[]{7}- 2} x = \frac{1}{\sqrt[]{7}- 2}](/latexrender/pictures/e703f7c2416ddf47e08bf87c1d414070.png)
racionalizando teremos:
![x = \sqrt[]{7}+ 2 x = \sqrt[]{7}+ 2](/latexrender/pictures/ba605a63f7946c831a78007188f2a3e8.png)
Temos portanto que
![\sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2} \sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2}](/latexrender/pictures/8434073fab6ba9d958ac1eec08c01c00.png)
Ai tu pega o primeiro resultado obtido, ou seja,
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
é um número compreendido entre 4 e 5, portanto
![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png)
com y > 1
De
![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png)
decorre que
![\sqrt[]{7}+ 2 - 4 = \frac{1}{y} \sqrt[]{7}+ 2 - 4 = \frac{1}{y}](/latexrender/pictures/d745d7b5ba75d3caffe8c114c4fbdca5.png)
![\sqrt[]{7} - 2 = \frac{1}{y} \sqrt[]{7} - 2 = \frac{1}{y}](/latexrender/pictures/53a2f29e9860608c52b9caf2d7b47658.png)
resumindo
![y = \sqrt[]{7}+ 2 y = \sqrt[]{7}+ 2](/latexrender/pictures/ab850b6eaca21bbe50e1e5e6c6b1cf31.png)
Fazendo a substituição no passo 2 teremos
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}}](/latexrender/pictures/e657bf4358b8934ea1d4cca81905a1fc.png)
Note que x = y =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
, se fossemos continuar o processo de y, encontrariamos w =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
e encontrariamos z =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
, e assim sucessivamente em um processo infinito. Segue portanto, que a fração contínua que representa
![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png)
será:
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/313a4f31c2a37f96b5b93a6fa1c58a9d.png)
é isso. tente entender, qualquer dúvida volte a perguntar


![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png) , a primeira coisa é descobrir o resultado da raíz está entre quais números inteiros. evidente que está entre 2 e 3, então escreveremos assim
, a primeira coisa é descobrir o resultado da raíz está entre quais números inteiros. evidente que está entre 2 e 3, então escreveremos assim![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png) com x > 1
com x > 1![\sqrt[]{7}- 2 = \frac{1}{x} \sqrt[]{7}- 2 = \frac{1}{x}](/latexrender/pictures/a2200a1972c4eb175e43e9481711087a.png)
![x = \frac{1}{\sqrt[]{7}- 2} x = \frac{1}{\sqrt[]{7}- 2}](/latexrender/pictures/e703f7c2416ddf47e08bf87c1d414070.png) racionalizando teremos:
racionalizando teremos: ![x = \sqrt[]{7}+ 2 x = \sqrt[]{7}+ 2](/latexrender/pictures/ba605a63f7946c831a78007188f2a3e8.png)
![\sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2} \sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2}](/latexrender/pictures/8434073fab6ba9d958ac1eec08c01c00.png)
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png) é um número compreendido entre 4 e 5, portanto
é um número compreendido entre 4 e 5, portanto![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png) com y > 1
com y > 1![\sqrt[]{7}+ 2 - 4 = \frac{1}{y} \sqrt[]{7}+ 2 - 4 = \frac{1}{y}](/latexrender/pictures/d745d7b5ba75d3caffe8c114c4fbdca5.png)
![\sqrt[]{7} - 2 = \frac{1}{y} \sqrt[]{7} - 2 = \frac{1}{y}](/latexrender/pictures/53a2f29e9860608c52b9caf2d7b47658.png)
![y = \sqrt[]{7}+ 2 y = \sqrt[]{7}+ 2](/latexrender/pictures/ab850b6eaca21bbe50e1e5e6c6b1cf31.png)
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}}](/latexrender/pictures/e657bf4358b8934ea1d4cca81905a1fc.png)
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/313a4f31c2a37f96b5b93a6fa1c58a9d.png)




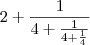
![\sqrt[]{5}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{5}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/639ca9de055d9801c6be7eda9464f674.png)
 :
: com
com 

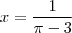


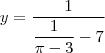

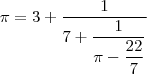

 . Como que eu faço?
. Como que eu faço?