Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por antonybel » Sex Nov 11, 2011 21:54
por antonybel » Sex Nov 11, 2011 21:54
Quatro operários fizeram um determinado numero total de horas extras no ùltimo mês. Sabe-se que Luís fez 1/5 desse total, que Mário fez o triplo de Luís, que João fez 1/3 do que Luís fez e que Otávio fez 5 horas extras. Pode se concluir, então, que o número de horas extras que Mário fez nesse mês foi?
bem, entendo que :
luiz = x/5
Mário= 3x/5
minha duvida é com João. No caso é fração de fração : 1/3 de 1/5 no caso seria matem-se a primeira e inverte-se a segunda e multiplica ? o que daria 3/5 . O que está errado neste raciocinio?
-
antonybel
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sex Nov 11, 2011 10:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por augusto0710 » Sex Nov 11, 2011 22:24
por augusto0710 » Sex Nov 11, 2011 22:24
Olá Antony, o seu raciocínio quanto ao

de

, porém quando vc tem

de

isto é igual a

, o que te dá como resultado
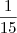
pois nesta multiplicação fazemos o produto do numerador com numerador e denominador com denominador.
Nós mantemos a primeira e multiplicamos pelo inverso da segunda quando temos divisão de frações, ok?
Espero ter ajudado
-
augusto0710
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 11, 2011 21:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por antonybel » Qua Nov 16, 2011 08:33
por antonybel » Qua Nov 16, 2011 08:33
Valeu, esclareceu legal. è que achei que 1/3 de 1/5 era uma divisão.
-
antonybel
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sex Nov 11, 2011 10:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3800 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- problema com fração!
por leandro moraes » Ter Jan 19, 2010 18:37
- 5 Respostas
- 4831 Exibições
- Última mensagem por Elcioschin

Qui Jan 21, 2010 15:09
Estatística
-
- problema de fração
por hevhoram » Qua Jun 02, 2010 20:28
- 1 Respostas
- 2287 Exibições
- Última mensagem por MarceloFantini

Qui Jun 03, 2010 03:28
Álgebra Elementar
-
- Problema com fração
por junior_gyn » Dom Abr 24, 2011 15:52
- 2 Respostas
- 4425 Exibições
- Última mensagem por NMiguel

Dom Abr 24, 2011 16:31
Desafios Médios
-
- Problema com fração
por junior_gyn » Dom Abr 24, 2011 16:55
- 1 Respostas
- 2754 Exibições
- Última mensagem por NMiguel

Dom Abr 24, 2011 17:16
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 de
de  , porém quando vc tem
, porém quando vc tem  , o que te dá como resultado
, o que te dá como resultado 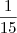 pois nesta multiplicação fazemos o produto do numerador com numerador e denominador com denominador.
pois nesta multiplicação fazemos o produto do numerador com numerador e denominador com denominador.

 .
.



