 por Aparecida » Seg Nov 14, 2011 14:11
por Aparecida » Seg Nov 14, 2011 14:11
Eu resolvi a fração continua de acordo com o caderno do aluno volume 1 da 8ª serie
Nessa apostila tem explicando passo a passo
-
Aparecida
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Dom Out 30, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por Francesca Vilanni » Seg Nov 14, 2011 14:51
por Francesca Vilanni » Seg Nov 14, 2011 14:51
Estrela_36 escreveu:Oi Francesca,
Foi assim que resolvi.
Agora estou em dúvida na letra e . Se puder confirmar sua resposta, seria de grande ajuda.
Respostas:
1) 1/xy = +6
2)
a) {x ? R/ -3 < x < 1/2 }
b) {x ? R/ x > 1}
c) {x ? R/ - 3/2 < x < 1}
d) {x ? R/ x < 2 }
e) {x ? R/ x < 1 e x ? -2 }
Beijinhos,
Roberta
Francesca Vilanni escreveu:2x+3<4
x<1/2
1-x<4
x>-3
Daí intersecção entre as retas -3<x<1/2
Acho que é só isso. Alguém confirma????
Olá Roberta,
Duas das suas soluções não confirmam com as minhas.
2) a) -3<x<1/2
b) conjunto vazio
c) -3/2<x<1
d) conjunto vazio
e) x<1 e x diferente -2
-
Francesca Vilanni
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Out 22, 2011 22:31
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por bbalthazar » Seg Nov 14, 2011 15:37
por bbalthazar » Seg Nov 14, 2011 15:37
Oi Silvia, pode me ajudar com as frações contínuas?
Veja seu email, fiz observações de dúvidas, se puder me responda! Não consegui entender nada!
Obrigada! Bjos!
"silvia fillet"]pessoal, eu tambem cheguei aos seguintes resultados:
1) 1/xy = +6
2)
a) {x ? R/ -3 < x < 1/2 }
b) {x ? R/ x > 1}
c) {x ? R/ - 3/2 < x < 1}
d) {x ? R/ x < 2 }
e) {x ? R/ x < 1 e x ? -2
Atividade 6 d1 ja resolvi[/quote]
-
bbalthazar
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Out 22, 2011 18:08
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lucinei daliberto » Seg Nov 14, 2011 15:58
por lucinei daliberto » Seg Nov 14, 2011 15:58
Estrela_36 escreveu:Oi Francesca,
Foi assim que resolvi.
Agora estou em dúvida na letra e . Se puder confirmar sua resposta, seria de grande ajuda.
Respostas:
1) 1/xy = +6
2)
a) {x ? R/ -3 < x < 1/2 }
b) {x ? R/ x > 1}
c) {x ? R/ - 3/2 < x < 1}
d) {x ? R/ x < 2 }
e) {x ? R/ x < 1 e x ? -2 }
Beijinhos,
Roberta
Francesca Vilanni escreveu:2x+3<4
x<1/2
1-x<4
x>-3
Daí intersecção entre as retas -3<x<1/2
Acho que é só isso. Alguém confirma????
Oi Roberta tambem faço parte da Redefor vou conferir a letra d e a letra e porque a a minha resolução da d) deu x>2e x<-2 e a letra e f(x) = -2 e g(x) = -2 mas vou conferir e se fosse possivel me passa confirma se voce elevou ao quadrado as questou da 1.
abraços.
Lucinei.
-
lucinei daliberto
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qua Out 26, 2011 16:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por lucinei daliberto » Seg Nov 14, 2011 16:02
por lucinei daliberto » Seg Nov 14, 2011 16:02
Cesar escreveu:lucinei daliberto escreveu:Oi alguem ja começou a atividade 6 poroque estou mais perdida do que cachorro em diade mudança.
Lucinei
eu começei se quiser ...
Oi Cesar acho que consegui resolver algumas como faço para conferir os resultados com voce, mando o meu e-mail ou pode ser pelo forum?
Abraços Lucinei
-
lucinei daliberto
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qua Out 26, 2011 16:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Miriam » Seg Nov 14, 2011 16:33
por Miriam » Seg Nov 14, 2011 16:33
silvia fillet escreveu:pessoal, eu tambem cheguei aos seguintes resultados:
1) 1/xy = +6
2)
a) {x ? R/ -3 < x < 1/2 }
b) {x ? R/ x > 1}
c) {x ? R/ - 3/2 < x < 1}
d) {x ? R/ x < 2 }
e) {x ? R/ x < 1 e x ? -2
Atividade 6 d1 ja resolvi
Olá!
Encontrei valores diferentes para b e d:
b) x > 1 ou x < -4
d) x > 2 ou x < -2
Será que errei alguma coisa? Talvez não tenha entendido direito a definição de min e max... Me ajudem!
-
Miriam
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Out 25, 2011 20:57
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por silvia fillet » Seg Nov 14, 2011 16:37
por silvia fillet » Seg Nov 14, 2011 16:37
Miriam, tambem nao tenho certeza dos resultados.
Qualquer coisa me envie um e-mail
silviafillet@gmail.comQuem sabe tiramos as duvidas
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por Estrela_36 » Seg Nov 14, 2011 17:00
por Estrela_36 » Seg Nov 14, 2011 17:00
lucinei daliberto escreveu:Estrela_36 escreveu:Oi Francesca,
Foi assim que resolvi.
Agora estou em dúvida na letra e . Se puder confirmar sua resposta, seria de grande ajuda.
Respostas:
1) 1/xy = +6
2)
a) {x ? R/ -3 < x < 1/2 }
b) {x ? R/ x > 1}
c) {x ? R/ - 3/2 < x < 1}
d) {x ? R/ x < 2 }
e) {x ? R/ x < 1 e x ? -2 }
Beijinhos,
Roberta
Francesca Vilanni escreveu:2x+3<4
x<1/2
1-x<4
x>-3
Daí intersecção entre as retas -3<x<1/2
Acho que é só isso. Alguém confirma????
Oi Roberta tambem faço parte da Redefor vou conferir a letra d e a letra e porque a a minha resolução da d) deu x>2e x<-2 e a letra e f(x) = -2 e g(x) = -2 mas vou conferir e se fosse possivel me passa confirma se voce elevou ao quadrado as questou da 1.
abraços.
Lucinei.
Oi Lucinei, elevei ao quadrado sim a expressão da questão 1
Primeiro vc eleva a equação x²+y²=1 ao quadradoo... dai vc vai ter o x^4+y^4.. que dá pra vc substituir por 17/18.. e resolve..
Quanto ao exercício 2, com os resultados aqui postados, fiquei confusa. Eu vi nos exemplos e resolvi tanto o max como o min da mesma forma, gerando duas inequações e fazendo a intersecção entre elas. Sera assim????
-
Estrela_36
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Out 22, 2011 23:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por silvia fillet » Seg Nov 14, 2011 17:09
por silvia fillet » Seg Nov 14, 2011 17:09
Lucilei, como voce resolveu o exercicio 2 max e min.
Pode me ajudar.
obrigada
Silvia e-mail
silviafillet@gmail.com
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por silvia fillet » Seg Nov 14, 2011 17:09
por silvia fillet » Seg Nov 14, 2011 17:09
ops Lucinei
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por silvia fillet » Seg Nov 14, 2011 17:10
por silvia fillet » Seg Nov 14, 2011 17:10
ops Lucinei
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por Aparecida » Seg Nov 14, 2011 17:28
por Aparecida » Seg Nov 14, 2011 17:28
Oi Lucinei, eu cheguei no mesmo resultado da letra d e b, mas nao estou conseguindo explicar onde esta o ponto máximo e o ponto mínimo.
Voce pode me ajudar
-
Aparecida
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Dom Out 30, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por silvia fillet » Seg Nov 14, 2011 17:33
por silvia fillet » Seg Nov 14, 2011 17:33
Aparecida e Lucinei, tambem estou com dificuldade de achar o max e o min.
Caso precisem da resoluçao da atividade 6 D1, ja tenho ela inteira resolvida, e so enviar um e-mail para mim
silviafillet@gmail.com
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por Alesilveira » Seg Nov 14, 2011 18:31
por Alesilveira » Seg Nov 14, 2011 18:31
resolvi o exercicio 2 e as questões b e d não estão batendo o resultado da minha b foi x>1 e x<-4 e a resposta da d foi
x+3>1-2x
x+2x<1-3
3x<-2
x<-2/3
1-2x>x+3
-2x-x>3-1
-3x>2
-x>2/3
x>-2/3
Se x for >-2/3 temos
x+3>5
x>5-3
x>2
Se x for < -2/3 temos
1-2x< 5
-2x< 5-1
-2x<4
-x<4/2
-x < 2
x>2
E estou com duvida nas questões da disciplina 1 será que alguém poderia dar uma luz.
-
Alesilveira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Out 23, 2011 11:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica/fisica
- Andamento: formado
 por soraya santiago » Seg Nov 14, 2011 20:48
por soraya santiago » Seg Nov 14, 2011 20:48
Pessoal ,
Ainda não entendi o exercício 1 da atividade 6, alguém pode me ajudar?
-
soraya santiago
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Nov 14, 2011 20:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Aparecida » Seg Nov 14, 2011 21:16
por Aparecida » Seg Nov 14, 2011 21:16
Alesilveira escreveu:resolvi o exercicio 2 e as questões b e d não estão batendo o resultado da minha b foi x>1 e x<-4 e a resposta da d foi
x+3>1-2x
x+2x<1-3
3x<-2
x<-2/3
1-2x>x+3
-2x-x>3-1
-3x>2
-x>2/3
x>-2/3
Se x for >-2/3 temos
x+3>5
x>5-3
x>2
Se x for < -2/3 temos
1-2x< 5
-2x< 5-1
-2x<4
-x<4/2
-x < 2
x>2
E estou com duvida nas questões da disciplina 1 será que alguém poderia dar uma luz.
Voce deve ter o caderno do professor volume 1 da 8ª serie, nessa apostila tem explicando passo a passo como resolve uma fração continua, ou no material de apoio a tutora colocou exemplos como resolver.
-
Aparecida
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Dom Out 30, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por Francesca Vilanni » Seg Nov 14, 2011 21:17
por Francesca Vilanni » Seg Nov 14, 2011 21:17
Fiz com régua e compasso o seguinte:
Reta com 7 unidades de medidas, na unidade 3 uma perpendicular de 2 unidades. Traço o triangulo retangulo de cateos 2 e 3 e hipotenusa raiz de 13.
Projeto essa hipotenusa sobre a reta marcando essa medida. A partir dessa medida raiz de 13 acrescento mais 3 unidades. Tenho os extremos 0 e 3 + raizde13, daí traço a mediatriz, com a abertura do compasso mais que a metade nos extremos. A mediatriz é o ponto desejado.
Espero ter ajudado.
F
-
Francesca Vilanni
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Out 22, 2011 22:31
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por larinha » Seg Nov 14, 2011 21:43
por larinha » Seg Nov 14, 2011 21:43
silvia fillet escreveu:Aparecida e Lucinei, tambem estou com dificuldade de achar o max e o min.
Caso precisem da resoluçao da atividade 6 D1, ja tenho ela inteira resolvida, e so enviar um e-mail para mim
silviafillet@gmail.com
Oi!
Nessa atividade 2 da 6, estou perdida com relação a max e min.
alguém poderia me ajudar? agradeço.
-
larinha
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Out 21, 2011 21:12
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por elianequicolli » Seg Nov 14, 2011 22:57
por elianequicolli » Seg Nov 14, 2011 22:57
larinha escreveu:silvia fillet escreveu:Aparecida e Lucinei, tambem estou com dificuldade de achar o max e o min.
Caso precisem da resoluçao da atividade 6 D1, ja tenho ela inteira resolvida, e so enviar um e-mail para mim
silviafillet@gmail.com
Oi!
Nessa atividade 2 da 6, estou perdida com relação a max e min.
alguém poderia me ajudar? agradeço.
Talvez possa ajudar:
Dada a importância de suas questões estou enviando sugestão a todos.
É algo assim:
Se se quer que max{a,b} max{a,b}<k, então a<k E b<k. Então resolva usando "e", isto é a intercecção entre as duas soluções, intercecção dos "varais".
Se for min{a,b}<t, então a<t OU b<t. Observe que é verdadeira e não precisa que os dois sejam menores que 5, basta que um OU o outro valor seja menor que 5. Então é a união das duas soluções, isto é, a união dos dois "varais".
Para max{a,b}>c, então se 'a' for o máximo e for maior que c já está correta a solução, a mesma coisa pensando em b.
Espero ter ajudado e não ter me confundido com tantas desigualdades e conectivos!
>
>
>
>
> -
>
>
>
>
>
> E
>
>
>
>
> ar
-
elianequicolli
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Out 17, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por Estrela_36 » Seg Nov 14, 2011 23:29
por Estrela_36 » Seg Nov 14, 2011 23:29
elianequicolli escreveu:larinha escreveu:silvia fillet escreveu:Aparecida e Lucinei, tambem estou com dificuldade de achar o max e o min.
Caso precisem da resoluçao da atividade 6 D1, ja tenho ela inteira resolvida, e so enviar um e-mail para mim
silviafillet@gmail.com
Oi!
Nessa atividade 2 da 6, estou perdida com relação a max e min.
alguém poderia me ajudar? agradeço.
Talvez possa ajudar:
Dada a importância de suas questões estou enviando sugestão a todos.
É algo assim:
Se se quer que max{a,b} max{a,b}<k, então a<k E b<k. Então resolva usando "e", isto é a intercecção entre as duas soluções, intercecção dos "varais".
Se for min{a,b}<t, então a<t OU b<t. Observe que é verdadeira e não precisa que os dois sejam menores que 5, basta que um OU o outro valor seja menor que 5. Então é a união das duas soluções, isto é, a união dos dois "varais".
Para max{a,b}>c, então se 'a' for o máximo e for maior que c já está correta a solução, a mesma coisa pensando em b.
Espero ter ajudado e não ter me confundido com tantas desigualdades e conectivos!
>
>
>
>
> -
>
>
>
>
>
> E
>
>
>
>
> ar
Ah.. então entendi..
Vou refazer minha atividade então.
Obrigada,
Roberta
-
Estrela_36
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Out 22, 2011 23:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por lucinei daliberto » Ter Nov 15, 2011 07:35
por lucinei daliberto » Ter Nov 15, 2011 07:35
Aparecida escreveu:Eu resolvi a fração continua de acordo com o caderno do aluno volume 1 da 8ª serie
Nessa apostila tem explicando passo a passo
Oi Aparecida não tenho esta apostila voce pode me dar uma luz porque estou perdida. Da disciplina 2 o exercicio 1 eu elevei ao quadrado mas não chego a um resultado coerente no exercicio 2 eu resolvi so tenho duvida na questa "e".
o e-mail é
lucinei_daliberto@yahoo.com.brEspero sua resposta, Abraços Lucinei
-
lucinei daliberto
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qua Out 26, 2011 16:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por lucinei daliberto » Ter Nov 15, 2011 07:38
por lucinei daliberto » Ter Nov 15, 2011 07:38
silvia fillet escreveu:ops Lucinei
Ja enviei para o e-mail espero ter ajudado.
-
lucinei daliberto
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qua Out 26, 2011 16:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por lucinei daliberto » Ter Nov 15, 2011 08:09
por lucinei daliberto » Ter Nov 15, 2011 08:09
Miriam escreveu:silvia fillet escreveu:pessoal, eu tambem cheguei aos seguintes resultados:
1) 1/xy = +6
2)
a) {x ? R/ -3 < x < 1/2 }
b) {x ? R/ x > 1}
c) {x ? R/ - 3/2 < x < 1}
d) {x ? R/ x < 2 }
e) {x ? R/ x < 1 e x ? -2
Atividade 6 d1 ja resolvi
Olá!
Encontrei valores diferentes para b e d:
b) x > 1 ou x < -4
d) x > 2 ou x < -2
Será que errei alguma coisa? Talvez não tenha entendido direito a definição de min e max... Me ajudem!
silvia fillet escreveu:ops Lucinei
Oi Miriam, na questão 1 não consigo chegar ao 1/xy=+6 voce pode me ajudar e em relação a:
b) -4<x>1
d)-2<x>2
Na questão e) ainda bem que conferi com a sua eu tinha errado na divisão, que vergonha,
agora vou tentar resolver ativ. 6 D1.
Abraços Lucinei
-
lucinei daliberto
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qua Out 26, 2011 16:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por lucinei daliberto » Ter Nov 15, 2011 09:01
por lucinei daliberto » Ter Nov 15, 2011 09:01
Estrela_36 escreveu:lucinei daliberto escreveu:Estrela_36 escreveu:Oi Francesca,
Foi assim que resolvi.
Agora estou em dúvida na letra e . Se puder confirmar sua resposta, seria de grande ajuda.
Respostas:
1) 1/xy = +6
2)
a) {x ? R/ -3 < x < 1/2 }
b) {x ? R/ x > 1}
c) {x ? R/ - 3/2 < x < 1}
d) {x ? R/ x < 2 }
e) {x ? R/ x < 1 e x ? -2 }
Beijinhos,
Roberta
Francesca Vilanni escreveu:2x+3<4
x<1/2
1-x<4
x>-3
Daí intersecção entre as retas -3<x<1/2
Acho que é só isso. Alguém confirma????
Oi Roberta tambem faço parte da Redefor vou conferir a letra d e a letra e porque a a minha resolução da d) deu x>2e x<-2 e a letra e f(x) = -2 e g(x) = -2 mas vou conferir e se fosse possivel me passa confirma se voce elevou ao quadrado as questou da 1.
abraços.
Lucinei.
Oi Lucinei, elevei ao quadrado sim a expressão da questão 1
Primeiro vc eleva a equação x²+y²=1 ao quadradoo... dai vc vai ter o x^4+y^4.. que dá pra vc substituir por 17/18.. e resolve..
Quanto ao exercício 2, com os resultados aqui postados, fiquei confusa. Eu vi nos exemplos e resolvi tanto o max como o min da mesma forma, gerando duas inequações e fazendo a intersecção entre elas. Sera assim????
Sim é exatamente isto que eu fiz, so estou mandando um correia para a minha coordenadora se temos que mandar a reta tambem ou somente colocar os resultados.
Eu ja tinha elevado ao quadrado da forma que voce fez mas acho que estou substiruindo errado vou tentar novamente, porque não chego ao seu resultado, o meu da zero, se eu não conseguir vou pedir que me diga onde substituir, porque acho que estou com a cabeça tão quente que as vezes não enxergamos o obvio, isso acontece com voce tambem?
abraços Lucinei.
-
lucinei daliberto
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qua Out 26, 2011 16:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Estrela_36 » Ter Nov 15, 2011 10:36
por Estrela_36 » Ter Nov 15, 2011 10:36
lucinei daliberto escreveu:Estrela_36 escreveu:lucinei daliberto escreveu:Estrela_36 escreveu:Oi Francesca,
Foi assim que resolvi.
Agora estou em dúvida na letra e . Se puder confirmar sua resposta, seria de grande ajuda.
Respostas:
1) 1/xy = +6
2)
a) {x ? R/ -3 < x < 1/2 }
b) {x ? R/ x > 1}
c) {x ? R/ - 3/2 < x < 1}
d) {x ? R/ x < 2 }
e) {x ? R/ x < 1 e x ? -2 }
Beijinhos,
Roberta
Francesca Vilanni escreveu:2x+3<4
x<1/2
1-x<4
x>-3
Daí intersecção entre as retas -3<x<1/2
Acho que é só isso. Alguém confirma????
Oi Roberta tambem faço parte da Redefor vou conferir a letra d e a letra e porque a a minha resolução da d) deu x>2e x<-2 e a letra e f(x) = -2 e g(x) = -2 mas vou conferir e se fosse possivel me passa confirma se voce elevou ao quadrado as questou da 1.
abraços.
Lucinei.
Oi Lucinei, elevei ao quadrado sim a expressão da questão 1
Primeiro vc eleva a equação x²+y²=1 ao quadradoo... dai vc vai ter o x^4+y^4.. que dá pra vc substituir por 17/18.. e resolve..
Quanto ao exercício 2, com os resultados aqui postados, fiquei confusa. Eu vi nos exemplos e resolvi tanto o max como o min da mesma forma, gerando duas inequações e fazendo a intersecção entre elas. Sera assim????
Sim é exatamente isto que eu fiz, so estou mandando um correia para a minha coordenadora se temos que mandar a reta tambem ou somente colocar os resultados.
Eu ja tinha elevado ao quadrado da forma que voce fez mas acho que estou substiruindo errado vou tentar novamente, porque não chego ao seu resultado, o meu da zero, se eu não conseguir vou pedir que me diga onde substituir, porque acho que estou com a cabeça tão quente que as vezes não enxergamos o obvio, isso acontece com voce tambem?
abraços Lucinei.
Oi Lucinei..
Resolvi o exercício da seguinte maneira


Agrupamos o


Sabemos que

Portanto substituímos este valor na expressão:


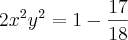

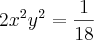
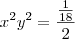
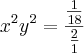
Multiplicando os meios e os extremos, temos:

![xy ={+}_{-}\sqrt[2]{\frac{1}{36}} xy ={+}_{-}\sqrt[2]{\frac{1}{36}}](/latexrender/pictures/426a9408cb3c0975247d84f10790c26b.png)
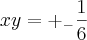
De acordo com o enunciado x e y são números reais positivos, portanto CONSIDERAREMOS somente a resposta positiva.
Concluímos então que o valor de
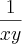
é:

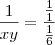
Multiplicando os meios e os extremos, temos:

-
Estrela_36
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Out 22, 2011 23:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por silvia fillet » Ter Nov 15, 2011 10:42
por silvia fillet » Ter Nov 15, 2011 10:42
Esta correta a resoluçao.
Silvia
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por Alesilveira » Ter Nov 15, 2011 11:02
por Alesilveira » Ter Nov 15, 2011 11:02
Infelizmente eu não tenho o material da oitava serie se alguem poder me enviar o meu e-mail é
silveirale@superig.com.br. Obrigada
-
Alesilveira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Out 23, 2011 11:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica/fisica
- Andamento: formado
 por silvia fillet » Ter Nov 15, 2011 11:16
por silvia fillet » Ter Nov 15, 2011 11:16
eu tenho o caderno do aluno com a resposta de ajuda:
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por lucinei daliberto » Ter Nov 15, 2011 15:41
por lucinei daliberto » Ter Nov 15, 2011 15:41
Estrela_36 escreveu:lucinei daliberto escreveu:Estrela_36 escreveu:lucinei daliberto escreveu:Estrela_36 escreveu:Oi Francesca,
Foi assim que resolvi.
Agora estou em dúvida na letra e . Se puder confirmar sua resposta, seria de grande ajuda.
Respostas:
1) 1/xy = +6
2)
a) {x ? R/ -3 < x < 1/2 }
b) {x ? R/ x > 1}
c) {x ? R/ - 3/2 < x < 1}
d) {x ? R/ x < 2 }
e) {x ? R/ x < 1 e x ? -2 }
Beijinhos,
Roberta
Francesca Vilanni escreveu:2x+3<4
x<1/2
1-x<4
x>-3
Daí intersecção entre as retas -3<x<1/2
Acho que é só isso. Alguém confirma????
Oi Roberta tambem faço parte da Redefor vou conferir a letra d e a letra e porque a a minha resolução da d) deu x>2e x<-2 e a letra e f(x) = -2 e g(x) = -2 mas vou conferir e se fosse possivel me passa confirma se voce elevou ao quadrado as questou da 1.
abraços.
Lucinei.
Oi Lucinei, elevei ao quadrado sim a expressão da questão 1
Primeiro vc eleva a equação x²+y²=1 ao quadradoo... dai vc vai ter o x^4+y^4.. que dá pra vc substituir por 17/18.. e resolve..
Quanto ao exercício 2, com os resultados aqui postados, fiquei confusa. Eu vi nos exemplos e resolvi tanto o max como o min da mesma forma, gerando duas inequações e fazendo a intersecção entre elas. Sera assim????
Sim é exatamente isto que eu fiz, so estou mandando um correia para a minha coordenadora se temos que mandar a reta tambem ou somente colocar os resultados.
Eu ja tinha elevado ao quadrado da forma que voce fez mas acho que estou substiruindo errado vou tentar novamente, porque não chego ao seu resultado, o meu da zero, se eu não conseguir vou pedir que me diga onde substituir, porque acho que estou com a cabeça tão quente que as vezes não enxergamos o obvio, isso acontece com voce tambem?
abraços Lucinei.
Oi Lucinei..
Resolvi o exercício da seguinte maneira


Agrupamos o


Sabemos que

Portanto substituímos este valor na expressão:


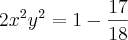

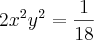
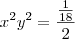
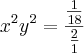
Multiplicando os meios e os extremos, temos:

![xy ={+}_{-}\sqrt[2]{\frac{1}{36}} xy ={+}_{-}\sqrt[2]{\frac{1}{36}}](/latexrender/pictures/426a9408cb3c0975247d84f10790c26b.png)
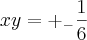
De acordo com o enunciado x e y são números reais positivos, portanto CONSIDERAREMOS somente a resposta positiva.
Concluímos então que o valor de
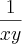
é:

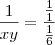
Multiplicando os meios e os extremos, temos:

Eu estava elevando ao quadrado mas não colocava em produtos notaveis, eu elevava separado por este motivo o resultado davan zero.
Muito obrigado
Abraços Lucinei
-
lucinei daliberto
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qua Out 26, 2011 16:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Alesilveira » Ter Nov 15, 2011 17:32
por Alesilveira » Ter Nov 15, 2011 17:32
Se alguem puder mandar o material da atividade 6 para mim o meu e-mail é
silveirale@superig.com.br
-
Alesilveira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Out 23, 2011 11:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica/fisica
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- números: racionais
por Victor Gabriel » Dom Mai 12, 2013 14:35
- 0 Respostas
- 3222 Exibições
- Última mensagem por Victor Gabriel

Dom Mai 12, 2013 14:35
Álgebra Elementar
-
- Conjunto dos números racionais.
por scggomes » Sex Fev 18, 2011 10:38
- 4 Respostas
- 77708 Exibições
- Última mensagem por scggomes

Sex Fev 18, 2011 16:17
Álgebra Elementar
-
- Adição e Subtração de números racionais
por LuizCarlos » Sex Mar 16, 2012 20:09
- 1 Respostas
- 4891 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 22:29
Álgebra Elementar
-
- Numero irracional entre numeros racionais
por Roni Martins » Qua Fev 24, 2010 10:36
- 1 Respostas
- 11936 Exibições
- Última mensagem por Molina

Qua Fev 24, 2010 13:18
Números Complexos
-
- problemas com expressões numeros inteiros e racionais.
por Julie » Qua Jul 28, 2010 10:00
- 3 Respostas
- 13428 Exibições
- Última mensagem por Firstlovi

Sex Jun 10, 2016 05:54
Tópicos sem Interação (leia as regras)
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

































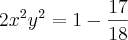

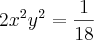
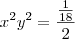
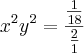

![xy ={+}_{-}\sqrt[2]{\frac{1}{36}} xy ={+}_{-}\sqrt[2]{\frac{1}{36}}](/latexrender/pictures/426a9408cb3c0975247d84f10790c26b.png)
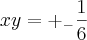
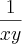 é:
é:
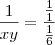





é:


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.