 quando a =2 e b=3 como sei que ela nao satisfaz o teorema?? como faço pra descobrir de maneira rapida?
quando a =2 e b=3 como sei que ela nao satisfaz o teorema?? como faço pra descobrir de maneira rapida?

 quando a =2 e b=3 como sei que ela nao satisfaz o teorema?? como faço pra descobrir de maneira rapida?
quando a =2 e b=3 como sei que ela nao satisfaz o teorema?? como faço pra descobrir de maneira rapida?
matmatco escreveu:olá, nao estou entendendo como faço pra saber qual funçao satisfaz o teorema do valor medio por exemploquando a =2 e b=3 como sei que ela nao satisfaz o teorema?? como faço pra descobrir de maneira rapida?
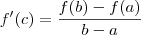 .
. e o intervalo [2, 3]. Ela atende as duas hipóteses do teorema:
e o intervalo [2, 3]. Ela atende as duas hipóteses do teorema:

matmatco escreveu:entao eu tenho que pegar valores entre o intervalo como no exemplo [2,3] e verificar se ele tbm é derivavel é isso??
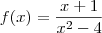 , você precisa ser capaz de reconhecer que ela é contínua e derivável para todo x real, exceto para x = -2 e x = 2. Sendo assim, para qualquer intervalo [a, b] que não contenha nem -2 e nem 2, essa função irá atender ao Teorema do Valor Médio nesse intervalo.
, você precisa ser capaz de reconhecer que ela é contínua e derivável para todo x real, exceto para x = -2 e x = 2. Sendo assim, para qualquer intervalo [a, b] que não contenha nem -2 e nem 2, essa função irá atender ao Teorema do Valor Médio nesse intervalo.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

