 por Ana_Rodrigues » Seg Nov 14, 2011 10:02
por Ana_Rodrigues » Seg Nov 14, 2011 10:02
A área de um triângulo equilátero decresce à razão de 4cm^2/min. Determine a taxa na qual o comprimento do lado está variando quando a área do triângulo é 200cm^2.
sei que
A=(b.h)/2
Não consegui desenvolver essa formula pra encontrar o que pede a questão!
Agradeço desde já a quem me ajudar a entender como se faz isso!
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ana_Rodrigues » Seg Nov 14, 2011 11:43
por Ana_Rodrigues » Seg Nov 14, 2011 11:43
Olá, eu tentei fazer essa questão e gostaria de saber se está correta. A resposta bate com o gabarito, caso tenha outra forma de resolver essa questão peço a quem souber que mostre como resolve-la
dA/dt=4cm^2/min
A=200cm^2
Altura do triângulo
L^2=(L/2)^2 +h^2
h=(L?3)/2
Agora vou encontrar o lado quando a área é 200cm^2
A=
![\frac{\frac{l.l\sqrt[2]{3}}{2}}{2} \frac{\frac{l.l\sqrt[2]{3}}{2}}{2}](/latexrender/pictures/2969a1c880b827e62e17fe79413ea0b2.png)
L=
![\frac{20\sqrt[2]{2}\sqrt[4]{3}}{\sqrt[2]{3}} \frac{20\sqrt[2]{2}\sqrt[4]{3}}{\sqrt[2]{3}}](/latexrender/pictures/f68ba4b6305df5658291900dc164126a.png)
Agora vou encontrar a taxa
A=
![\frac{\frac{l.l\sqrt[2]{3}}{2}}{2} \frac{\frac{l.l\sqrt[2]{3}}{2}}{2}](/latexrender/pictures/2969a1c880b827e62e17fe79413ea0b2.png)
![\frac{dA}{dt}=\frac{\sqrt[2]{3}}{2}.l .\frac{dl}{dt}
[tex]\frac{dA}{dt}=\frac{\sqrt[2]{3}}{2}.\frac{20\sqrt[2]{2}\sqrt[4]{3}}{\sqrt[2]{3}}.\frac{dl}{dt} \frac{dA}{dt}=\frac{\sqrt[2]{3}}{2}.l .\frac{dl}{dt}
[tex]\frac{dA}{dt}=\frac{\sqrt[2]{3}}{2}.\frac{20\sqrt[2]{2}\sqrt[4]{3}}{\sqrt[2]{3}}.\frac{dl}{dt}](/latexrender/pictures/2e5d41a516aa37b6356fcd8db48cb1e3.png)
![\frac{dl}{dt}= \frac{\sqrt[2]{2}}{5\sqrt[4]{3}} \frac{dl}{dt}= \frac{\sqrt[2]{2}}{5\sqrt[4]{3}}](/latexrender/pictures/b00592347e19f782897ca45f74430882.png)
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Seg Nov 14, 2011 12:19
por LuizAquino » Seg Nov 14, 2011 12:19
Ana_Rodrigues escreveu:A área de um triângulo equilátero decresce à razão de 4cm^2/min. Determine a taxa na qual o comprimento do lado está variando quando a área do triângulo é 200cm^2.
Ana_Rodrigues escreveu:Olá, eu tentei fazer essa questão e gostaria de saber se está correta. A resposta bate com o gabarito, caso tenha outra forma de resolver essa questão peço a quem souber que mostre como resolve-la
dA/dt=4cm^2/min
A=200cm^2
Altura do triângulo
L^2=(L/2)^2 +h^2
h=(L?3)/2
Agora vou encontrar o lado quando a área é 200cm^2
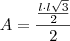
![L=\frac{20\sqrt{2}\sqrt[4]{3}}{\sqrt{3}} L=\frac{20\sqrt{2}\sqrt[4]{3}}{\sqrt{3}}](/latexrender/pictures/cbe55fbcb4b60340df36724d94667f17.png)
Agora vou encontrar a taxa
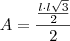
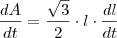
![\frac{dA}{dt}= \frac{\sqrt{3}}{2}\cdot \frac{20\sqrt{2}\sqrt[4]{3}}{\sqrt[2]{3}} \cdot \frac{dl}{dt} \frac{dA}{dt}= \frac{\sqrt{3}}{2}\cdot \frac{20\sqrt{2}\sqrt[4]{3}}{\sqrt[2]{3}} \cdot \frac{dl}{dt}](/latexrender/pictures/812e230655a5862e2eb119deb5d2e891.png)
![\frac{dl}{dt}= \frac{\sqrt{2}}{5\sqrt[4]{3}} \frac{dl}{dt}= \frac{\sqrt{2}}{5\sqrt[4]{3}}](/latexrender/pictures/111f6bed0fdc40ce4a2e9db1f4021f1c.png)
O caminho é esse mesmo. Entretanto, o exercício diz que a
área decresce à razão de 4 cm²/min (ou seja, diminuindo 4 cm² por minuto). Sendo assim, devemos ter

.
Como a área está
decrescendo com o tempo, faz sentido que o lado também esteja. No final, você vai encontrar que
![\frac{dl}{dt}= -\frac{\sqrt{2}}{5\sqrt[4]{3}} \frac{dl}{dt}= -\frac{\sqrt{2}}{5\sqrt[4]{3}}](/latexrender/pictures/f35275167f14ec33c384cd68a2711789.png)
.
Note que a reposta no gabarito deveria estar negativa.
ObservaçãoSe desejar revisar esse conteúdo, então eu gostaria de recomendar a vídeo-aula "18. Cálculo I - Taxas de Variação Relacionadas". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Taxas Relacionadas
por RonnieAlmeida » Qui Mai 22, 2014 16:48
- 0 Respostas
- 1459 Exibições
- Última mensagem por RonnieAlmeida

Qui Mai 22, 2014 16:48
Cálculo: Limites, Derivadas e Integrais
-
- Taxas Relacionadas
por RonnieAlmeida » Qui Mai 22, 2014 16:58
- 1 Respostas
- 2710 Exibições
- Última mensagem por alienante

Dom Jun 15, 2014 07:59
Cálculo: Limites, Derivadas e Integrais
-
- Taxas relacionadas
por Lorijuca » Qui Mai 29, 2014 22:23
- 0 Respostas
- 2952 Exibições
- Última mensagem por Lorijuca

Qui Mai 29, 2014 22:23
Cálculo: Limites, Derivadas e Integrais
-
- TAXAS RELACIONADAS
por Daniela[ » Sáb Jul 05, 2014 15:15
- 3 Respostas
- 6967 Exibições
- Última mensagem por young_jedi

Dom Jul 06, 2014 14:25
Cálculo: Limites, Derivadas e Integrais
-
- Taxas relacionadas
por Fernandobertolaccini » Sáb Out 25, 2014 09:57
- 5 Respostas
- 4575 Exibições
- Última mensagem por Fernandobertolaccini

Sáb Out 25, 2014 12:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\frac{\frac{l.l\sqrt[2]{3}}{2}}{2} \frac{\frac{l.l\sqrt[2]{3}}{2}}{2}](/latexrender/pictures/2969a1c880b827e62e17fe79413ea0b2.png)
![\frac{20\sqrt[2]{2}\sqrt[4]{3}}{\sqrt[2]{3}} \frac{20\sqrt[2]{2}\sqrt[4]{3}}{\sqrt[2]{3}}](/latexrender/pictures/f68ba4b6305df5658291900dc164126a.png)
![\frac{dA}{dt}=\frac{\sqrt[2]{3}}{2}.l .\frac{dl}{dt}
[tex]\frac{dA}{dt}=\frac{\sqrt[2]{3}}{2}.\frac{20\sqrt[2]{2}\sqrt[4]{3}}{\sqrt[2]{3}}.\frac{dl}{dt} \frac{dA}{dt}=\frac{\sqrt[2]{3}}{2}.l .\frac{dl}{dt}
[tex]\frac{dA}{dt}=\frac{\sqrt[2]{3}}{2}.\frac{20\sqrt[2]{2}\sqrt[4]{3}}{\sqrt[2]{3}}.\frac{dl}{dt}](/latexrender/pictures/2e5d41a516aa37b6356fcd8db48cb1e3.png)
![\frac{dl}{dt}= \frac{\sqrt[2]{2}}{5\sqrt[4]{3}} \frac{dl}{dt}= \frac{\sqrt[2]{2}}{5\sqrt[4]{3}}](/latexrender/pictures/b00592347e19f782897ca45f74430882.png)
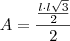
![L=\frac{20\sqrt{2}\sqrt[4]{3}}{\sqrt{3}} L=\frac{20\sqrt{2}\sqrt[4]{3}}{\sqrt{3}}](/latexrender/pictures/cbe55fbcb4b60340df36724d94667f17.png)
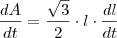
![\frac{dA}{dt}= \frac{\sqrt{3}}{2}\cdot \frac{20\sqrt{2}\sqrt[4]{3}}{\sqrt[2]{3}} \cdot \frac{dl}{dt} \frac{dA}{dt}= \frac{\sqrt{3}}{2}\cdot \frac{20\sqrt{2}\sqrt[4]{3}}{\sqrt[2]{3}} \cdot \frac{dl}{dt}](/latexrender/pictures/812e230655a5862e2eb119deb5d2e891.png)
![\frac{dl}{dt}= \frac{\sqrt{2}}{5\sqrt[4]{3}} \frac{dl}{dt}= \frac{\sqrt{2}}{5\sqrt[4]{3}}](/latexrender/pictures/111f6bed0fdc40ce4a2e9db1f4021f1c.png)
 .
.![\frac{dl}{dt}= -\frac{\sqrt{2}}{5\sqrt[4]{3}} \frac{dl}{dt}= -\frac{\sqrt{2}}{5\sqrt[4]{3}}](/latexrender/pictures/f35275167f14ec33c384cd68a2711789.png) .
.