Caiu uma questão na Unesp 2012 1ª Fase e eu não a soube resolver. A Equação era: x³-3x²-x+K=0, para encontrar o valor do K, pra facilitar, aqui vai a imagem já com a resolução.

Meu problema é que eu não consigo entender como encontrar as raízes da equação do 3º Grau, eu observei a resolução e mesmo assim não consegui desvendar, por exemplo, em qualquer equação desse tipo, quando o coeficiente D não foi dado e é pedido para encontrá-lo, de onde veio veio aquele 3 ao qual a equação foi igualada? Tem como resolver ainda mais detalhadamente? Faz alguma diferença a informação de que é uma P.A.? Como o resultado de A=1?. E não tem nessa questão, mais e se pedisse todas as três raízes da equação, como encontrá-las?
Obrigado. Espero que tenha ficado claro e eu voltarei aqui para tentar entender.
Gostei do fórum, parece muito completo!


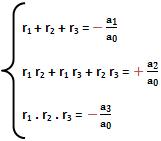
 ,
,  e
e  , onde
, onde  é a razão da progressão.
é a razão da progressão.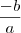 , onde
, onde  é o coeficiente do
é o coeficiente do  . Logo,
. Logo,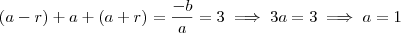 .
. , substituindo
, substituindo  teremos
teremos  .
.

