 por Richard Oliveira » Seg Nov 14, 2011 00:50
por Richard Oliveira » Seg Nov 14, 2011 00:50
Entendi, eu estava pulando uma parte no exercício.
Eu entendo e sei que vocês não passam o dia inteiro aqui, e já quero deixar bem claro: eu não estou achando que vocês são obrigados a fazer serviços pra mim, por isso que eu procuro ser o mais educado possível em minhas perguntas. Eu estou aqui no site perguntando, porque já é um site próprio para isso, e como eu tenho um sonho que desejo realizar, estou aqui tentando tirar minhas dúvidas. Em relação a meu segundo post, eu postei aquele comentário porque eu vi outro tópico mais novo sendo respondido antes do que o meu. Mas antes de mais nada, eu ressalto que quero ter uma boa relação no site, portanto eu serei humilde: mesmo não sendo respondido antes, acredito que eu devia ter esperado mais e assim farei nós próximos tópicos.
Obrigado pela resposta, consegui resolver.
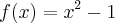 e
e 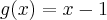 . A diferença entre as funções compostas
. A diferença entre as funções compostas é igual a:
é igual a: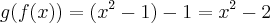
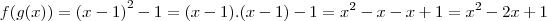
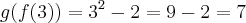
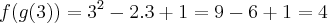
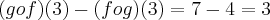

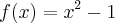 e
e 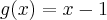 . A diferença entre as funções compostas
. A diferença entre as funções compostas é igual a:
é igual a: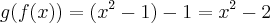
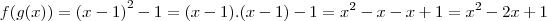
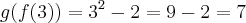
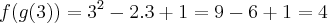
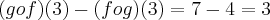


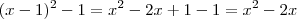 . Tente refazer.
. Tente refazer.



 .
.
 :
: