 por raquelcattelam » Sex Mai 15, 2009 15:16
por raquelcattelam » Sex Mai 15, 2009 15:16
Olá.
Meu filho recebu o seguinte problema para resolver e não consigo ajudá-lo.
Uma plataforma, inicilmente quadrada foi ampliada: 3 metros a mais em um dos lados e 2 metros a mais no outro. Sabendo que a área da plataforma ampliada é de 56 m quadrados, qual era a sua area inicial? A resposta que tem que dar é 25 metros quadrados. Obrigada pela ajuda
-
raquelcattelam
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mai 15, 2009 15:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
 por admin » Sex Mai 15, 2009 15:54
por admin » Sex Mai 15, 2009 15:54
Olá
raquelcattelam, boas-vindas!
O primeiro passo, você já deve ter feito, é o desenho:
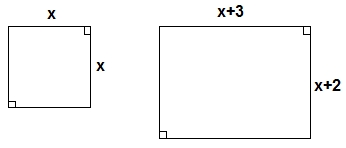
- plataformas.jpg (6.54 KiB) Exibido 4688 vezes
A área

da plataforma inicial é:

A área

da plataforma ampliada também pode ser escrita assim:
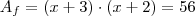
Faça a distributiva e ficará com a equação do segundo grau na forma geral:

Para mais informações sobre a "fórmula de Bhaskara", veja este tópico:
http://www.ajudamatematica.com/viewtopic.php?f=72&t=253&p=626Após obter o valor de

, calcule a resposta pedida

.
Comente as dúvidas!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por raquelcattelam » Sex Mai 15, 2009 20:04
por raquelcattelam » Sex Mai 15, 2009 20:04
Nossa, muito obrigada pela ajuda. Ele esta com bastante dificuldade nesse ponto...Adorei esse site...
-
raquelcattelam
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mai 15, 2009 15:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Fracionária do Segundo Grau Ajuda Urgente
 por karenblond » Ter Ago 18, 2015 11:17
por karenblond » Ter Ago 18, 2015 11:17
- 6 Respostas
- 8152 Exibições
- Última mensagem por nakagumahissao

Ter Ago 18, 2015 18:17
Equações
-
- EQUAÇÕES FRACIONARIAS DO 2° GRAU [AJUDA URGENTE!!!]
por rayanne_ » Ter Mai 13, 2014 00:43
- 1 Respostas
- 1500 Exibições
- Última mensagem por Russman

Qua Mai 14, 2014 00:54
Equações
-
- Ajuda Urgente com esse problema de função
por Mayedra » Ter Nov 17, 2015 16:33
- 0 Respostas
- 1636 Exibições
- Última mensagem por Mayedra

Ter Nov 17, 2015 16:33
Funções
-
- Problema equação do primeiro grau
por LuizCarlos » Sáb Abr 28, 2012 19:59
- 9 Respostas
- 4845 Exibições
- Última mensagem por DanielFerreira

Dom Abr 29, 2012 00:52
Equações
-
- [Equação do Primeiro Grau] Problema
por ALPC » Sáb Jan 19, 2013 14:51
- 4 Respostas
- 2359 Exibições
- Última mensagem por ALPC

Dom Jan 20, 2013 12:53
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 da plataforma inicial é:
da plataforma inicial é:
 da plataforma ampliada também pode ser escrita assim:
da plataforma ampliada também pode ser escrita assim: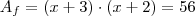

 , calcule a resposta pedida
, calcule a resposta pedida 


 , avisa que eu resolvo.
, avisa que eu resolvo.

