
Quando
 o declive da reta secante aproxima-se do declive da reta tangente a a.Ou seja do valor da derivada no ponto x=a.
o declive da reta secante aproxima-se do declive da reta tangente a a.Ou seja do valor da derivada no ponto x=a.Quando o calculo do limite não corre bem, as coisas começam a complicar-se!
Seja a função
 . Calcule-se o declive da reta tangente no ponto (1,2), utilizando a primeira formula:
. Calcule-se o declive da reta tangente no ponto (1,2), utilizando a primeira formula: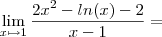
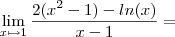

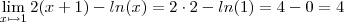
Seria de concluir que a derivada da função no ponto x=1 seria 4!!!
Mas quando calculo a derivada através das regras de diferenciação obtenho:

ou seja,

Em qual deles errei?
Após algumas simulações gráficas, verifiquei que foi no limite que errei, mas por mais que me esforce não sei onde.Podem ajudar-me?
Obrigado


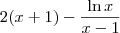 .
.

 resulta em
resulta em  quando se substituí
quando se substituí 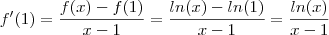
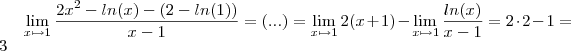
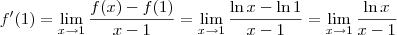
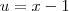 . Como
. Como  , teremos que
, teremos que 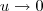 . Portanto, podemos escrever:
. Portanto, podemos escrever: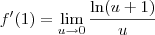

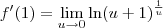
 , o limite poderá "entrar" na função:
, o limite poderá "entrar" na função:![f^\prime(1) =\ln \left[\lim_{u\to 0} (u+1)^{\frac{1}{u}}\right] f^\prime(1) =\ln \left[\lim_{u\to 0} (u+1)^{\frac{1}{u}}\right]](/latexrender/pictures/154d10a29b8f7b0bba9e026f2e5b1a43.png)



 .
.



