 por Adriana Saisse » Ter Nov 08, 2011 17:08
por Adriana Saisse » Ter Nov 08, 2011 17:08
NUMA VIAGEM, ADRIANE NOTOU QUE AO PARAR PELA PRIMEIRA VEZ O CARRO HAVIA GASTO 1/4 DO COMBUSTÍVEL?. AO PARAR PELA SEGUNDA VEZ, VERIFICOU QUE ENTRE A PRIMEIRA E SEGUNDA PARADA O CARRO HAVIA GASTO 2/3 DO COMBUSTÍVEL QUE SOBRARA NA PRIMEIRA PARADA. COLOCOU ,ENTÃO , 39 LITROS DE COMBUSTÍVEL E O TANQUE FICOU CHEIO.
A) QUAL A FRAÇÃO QUE CORRESPONDE A QUANTIDADE DE LITROS QUE RESTARAM NO TANQUE DA 1a PARADA?
(13:33:56) Adriana_Sai?sse: B) QUAL FRAÇÃO CORRESPONDE AO COMBUSTÍVEL GASTO NO PERCURSO DA 1a ATÉ A 2a PARADA?
(13:35:22) Adriana_Sai?sse: C) QUAL FRAÇÃO CORRESPONDE AO COMBUSTÍVEL GASTO DA SAÍDA ATÉ A 2a PARADA?
(13:36:03) Adriana_Sai?sse: D) QUAL FRAÇÃO CORRESPONDE AO COMBUSTÍVEL QUE HAVIA NO TANQUE NA 2a PARADA?
(13:36:35) Adriana_Sai?sse: E)QUANTOS LITROS CABEM NO TANQUE DO CARRO DE ADRIANE?
-
Adriana Saisse
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Nov 08, 2011 13:03
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Neperiano » Ter Nov 08, 2011 17:17
por Neperiano » Ter Nov 08, 2011 17:17
Ola
Gastou 25% do combustivel na primeira vez
Na segunda parada havia gasto 66%
Então no total gastou 25+66=91%
Então 91% é 39 litros logo
91 - 39
100 - x
x = 42,85 litros é 100% do tanque
Tente resolver agora as questões
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Adriana Saisse » Ter Nov 08, 2011 17:59
por Adriana Saisse » Ter Nov 08, 2011 17:59
Obrigada Neperiano, Foi uma questão de prova do Colégio Pedro II do 6 ano. E eu gostaria de ver outras resoluções. Atenciosamente, Adriana

-
Adriana Saisse
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Nov 08, 2011 13:03
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por MarceloFantini » Ter Nov 08, 2011 18:56
por MarceloFantini » Ter Nov 08, 2011 18:56
Cuja resolução está errada. Se gastou um quarto do tanque, sobrou
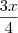
, onde x é o tanque cheio. Se gastou dois terços do que sobrou, então resta ao final

. Isto, adicionados 39 litros, é o tanque cheio e portanto
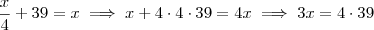
onde chegamos que
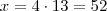
litros.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Adriana Saisse » Ter Nov 08, 2011 21:09
por Adriana Saisse » Ter Nov 08, 2011 21:09
ok Marcelo Fontini, vc é o cara a quem eu estava procurando. A solução do problema em fração :
a) 4/4 - 1/4 = 3/4
b) 2/3 * 3/4 = 1/2 ( não entendi o porque da multiplicação)
c) 1/4 + 1/2 = 3/4
d) 2/4
e) 3/4 = 39 , ou seja ;
39/3 = 13 * 4 = 52 litros
Esta correção foi feita pelo professor do Colégio Pedro II
A minha dúvida é o porque da multiplicação na resposta da letra b. Qdo o enunciado diz que: o carro havia gasto 2/3 de 3/4
E o início do enunciado diz que na 1a parada ele gastou 1/4 do combustível. Mas não diz qto havia no combustível de 4/4 e não informou que na saída o tanque estava cheio.
Atenciosamente, Adriana Saisse
-
Adriana Saisse
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Nov 08, 2011 13:03
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por MarceloFantini » Ter Nov 08, 2011 21:15
por MarceloFantini » Ter Nov 08, 2011 21:15
Se você não assumir que o tanque estava cheio, seu problema fica sem solução. É mal formulado, mas se você tentar resolver sem tomar essa hipótese provavelmente não conseguirá responder.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Adriana Saisse » Ter Nov 08, 2011 21:29
por Adriana Saisse » Ter Nov 08, 2011 21:29
ok, muito obrigada!

-
Adriana Saisse
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Nov 08, 2011 13:03
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por EMANUEL ROBSON » Qui Out 27, 2016 00:28
por EMANUEL ROBSON » Qui Out 27, 2016 00:28
Adriana Saisse escreveu:NUMA VIAGEM, ADRIANE NOTOU QUE AO PARAR PELA PRIMEIRA VEZ O CARRO HAVIA GASTO 1/4 DO COMBUSTÍVEL?. AO PARAR PELA SEGUNDA VEZ, VERIFICOU QUE ENTRE A PRIMEIRA E SEGUNDA PARADA O CARRO HAVIA GASTO 2/3 DO COMBUSTÍVEL QUE SOBRARA NA PRIMEIRA PARADA. COLOCOU ,ENTÃO , 39 LITROS DE COMBUSTÍVEL E O TANQUE FICOU CHEIO.
A) QUAL A FRAÇÃO QUE CORRESPONDE A QUANTIDADE DE LITROS QUE RESTARAM NO TANQUE DA 1a PARADA?
(13:33:56) Adriana_Sai?sse: B) QUAL FRAÇÃO CORRESPONDE AO COMBUSTÍVEL GASTO NO PERCURSO DA 1a ATÉ A 2a PARADA?
(13:35:22) Adriana_Sai?sse: C) QUAL FRAÇÃO CORRESPONDE AO COMBUSTÍVEL GASTO DA SAÍDA ATÉ A 2a PARADA?
(13:36:03) Adriana_Sai?sse: D) QUAL FRAÇÃO CORRESPONDE AO COMBUSTÍVEL QUE HAVIA NO TANQUE NA 2a PARADA?
(13:36:35) Adriana_Sai?sse: E)QUANTOS LITROS CABEM NO TANQUE DO CARRO DE ADRIANE?
GASTOU 1/4 DE 100% = 25%
GASTOU + 2/3 DO QUE SOBROU NA PRIMEIRA PARADA, LOGO, 100 - 25 = 75, 75.2/3 = 50%+25%= 75%
COLOCOU 39 LITROS E ENCHEU O TANQUE. SE 75% = 39 LITROS, 100% = X
75=39 75X=3.900, X= 3.900/75, X= 52 LITROS
100=X
-
EMANUEL ROBSON
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Out 27, 2016 00:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico de contabilidade
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3803 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- problema com fração!
por leandro moraes » Ter Jan 19, 2010 18:37
- 5 Respostas
- 4841 Exibições
- Última mensagem por Elcioschin

Qui Jan 21, 2010 15:09
Estatística
-
- problema de fração
por hevhoram » Qua Jun 02, 2010 20:28
- 1 Respostas
- 2289 Exibições
- Última mensagem por MarceloFantini

Qui Jun 03, 2010 03:28
Álgebra Elementar
-
- Problema com fração
por junior_gyn » Dom Abr 24, 2011 15:52
- 2 Respostas
- 4428 Exibições
- Última mensagem por NMiguel

Dom Abr 24, 2011 16:31
Desafios Médios
-
- Problema com fração
por junior_gyn » Dom Abr 24, 2011 16:55
- 1 Respostas
- 2755 Exibições
- Última mensagem por NMiguel

Dom Abr 24, 2011 17:16
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



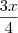 , onde x é o tanque cheio. Se gastou dois terços do que sobrou, então resta ao final
, onde x é o tanque cheio. Se gastou dois terços do que sobrou, então resta ao final  . Isto, adicionados 39 litros, é o tanque cheio e portanto
. Isto, adicionados 39 litros, é o tanque cheio e portanto 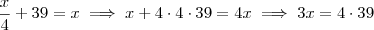 onde chegamos que
onde chegamos que 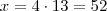 litros.
litros.



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.