 por Cleyson007 » Qua Mai 13, 2009 15:18
por Cleyson007 » Qua Mai 13, 2009 15:18
Olá, boa tarde!
Gostaria de saber se estou resolvendo corretamente a questão abaixo. Desde já, obrigado pela ajuda.
--> Determine o polinômio unitário: do 2º grau, sabendo que

é raiz e que

.
Resolvi assim: Polinômio unitário do 2º grau ->
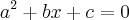
Sabendo que

é raiz:

(Equação I)
Sabendo que

-->
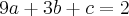
(Equação II)
A partir daqui não estou conseguindo desenvolver o raciocínio

Alguém pode me ajudar? Desde já agradeço pela ajuda.

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Qua Mai 13, 2009 22:50
por Molina » Qua Mai 13, 2009 22:50
Boa noite, Cleyson.
Se o polinômio é unitário (como informa o enunciado), o coeficiente do termo dominante (neste caso de x²) é igual a
1.
Um polinômio de segundo grau está na forma de

Mas como

que é o coeficiente do termo dominante, temos que:
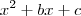
Beleza até aqui?
Agora considerando as outras informações do enuciado, temos:


Sendo assim:
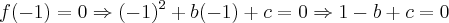 (equação 1)
(equação 1)e
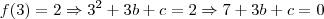
Agora dessas duas condições a cima temos que:

Substituindo na
(equação 1):
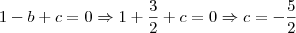 Logo, o polinômio fica:
Logo, o polinômio fica: 
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Qui Mai 14, 2009 11:07
por Cleyson007 » Qui Mai 14, 2009 11:07
Bom dia Diego Molina.
Primeiramente, muito obrigado por me ajudar

Sinceramente, fico muito feliz em saber que podemos compartihar conhecimentos. Como é bom conversar com pessoas que gostam do mesmo que gostamos (também sou apaixonado por Matemática)

--> Entendi o raciocínio da questão!! (Sua explicacão foi detalhada.. perfeita!!)
Obrigado amigo

Se precisar de algo.. se for do meu alcance, pode contar com minha ajuda

Um forte abraço.
Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Sex Mai 15, 2009 06:46
por Molina » Sex Mai 15, 2009 06:46
Opa!
De nada Cleyson.
Como você falou, fazemos isso porque gostamos.
O interessante é que algumas questões acabo tendo que ler o conteúdo novamente, já que não lembro com exatidão como que faz algum detalhe. E isso é bom! =)
Continuamos assim então.
Sei que um dia que precisar de vocês, também poderei contar.
Um grande abraço,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7155 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Polinômio
por Cleyson007 » Qua Jul 15, 2009 23:17
- 3 Respostas
- 2457 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 12:06
Polinômios
-
- polinomio
por Carolina0991 » Qui Jan 28, 2010 12:50
- 2 Respostas
- 2388 Exibições
- Última mensagem por MarceloFantini

Qui Jan 28, 2010 14:41
Polinômios
-
- polinomio
por Carolina0991 » Qui Jan 28, 2010 21:09
- 1 Respostas
- 1673 Exibições
- Última mensagem por Elcioschin

Qui Jan 28, 2010 22:42
Polinômios
-
- polinomio
por Carolina0991 » Qui Jan 28, 2010 21:20
- 1 Respostas
- 1253 Exibições
- Última mensagem por Elcioschin

Qui Jan 28, 2010 22:44
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é raiz e que
é raiz e que  .
.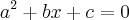
 é raiz:
é raiz:  (Equação I)
(Equação I) -->
--> 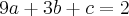 (Equação II)
(Equação II)





 que é o coeficiente do termo dominante, temos que:
que é o coeficiente do termo dominante, temos que: 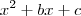

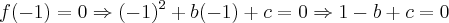
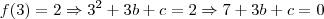

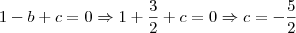





 , avisa que eu resolvo.
, avisa que eu resolvo.

