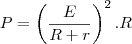Sub-seção para materiais das disciplinas relacionadas ao cálculo.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Suriano » Qua Mai 06, 2009 20:42
por Suriano » Qua Mai 06, 2009 20:42
1) Quando um resistor de R ohms é ligado aos terminais de uma bateria com uma força eletromotriz de E volts e uma resistência interna de r ohms, uma corrente de I ampères atravessa o circuito e dissipa uma potência de P watts, sendo
I = E / R + r;
P = I ^ 2 . R
Supondo que r seja constante, qual o valor de R para o qual a potência dissipada é máxima?
Estou com dificuldade para resolver o seguinte exercicio.
Já levei horas para chegar a solução mas não consegui. Conto com ajuda dos senhores(as).
Comecei substituindo o I = E / R + r na formula P = I ^ 2 . R para depois derivar....
Ficou P = (E / R + r) ^ 2 . R...
A partir daqui preciso de orientação.
Obrigado.
Suriano
-
Suriano
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 05, 2009 22:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia Analise de Sistemas
- Andamento: cursando
 por Molina » Qua Mai 06, 2009 22:30
por Molina » Qua Mai 06, 2009 22:30
Boa noite, Suriano.
Procure usar o
latex para escrever suas fórmular.
Confirme se é isso que precisa derivar:
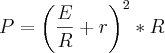
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Marcampucio » Qui Mai 07, 2009 16:50
por Marcampucio » Qui Mai 07, 2009 16:50
molina escreveu:Boa noite, Suriano.
Procure usar o
latex para escrever suas fórmular.
Confirme se é isso que precisa derivar:
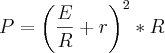
Abraços!

Olá molina,
A expressão é
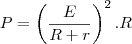
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Suriano » Qua Mai 13, 2009 21:39
por Suriano » Qua Mai 13, 2009 21:39
Molina, é isso mesmo, porém muito obrigado, o grupo de estudo conseguiu encontrar a solução.
Abraços.
Suriano.
-
Suriano
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 05, 2009 22:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia Analise de Sistemas
- Andamento: cursando
Voltar para Cálculo
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [derivada] Ponto minimo/máximo e concavidade
por gabriel feron » Dom Out 07, 2012 03:52
- 1 Respostas
- 2194 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 10:56
Cálculo: Limites, Derivadas e Integrais
-
- Otimização - Máximo e Mínimo
por elbert005 » Dom Jun 05, 2011 20:32
- 0 Respostas
- 4712 Exibições
- Última mensagem por elbert005

Dom Jun 05, 2011 20:32
Cálculo: Limites, Derivadas e Integrais
-
- Ponto Máximo
por Ana_Bela » Qui Nov 27, 2014 11:08
- 1 Respostas
- 1369 Exibições
- Última mensagem por adauto martins

Qui Nov 27, 2014 11:46
Funções
-
- Ponto Máximo e Mínimo de uma função.
por lucasowner » Qui Ago 13, 2015 03:05
- 1 Respostas
- 2001 Exibições
- Última mensagem por nakagumahissao

Qui Ago 13, 2015 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] extremos;ponto de minimo e maximo
por beel » Dom Out 30, 2011 19:15
- 2 Respostas
- 2137 Exibições
- Última mensagem por LuizAquino

Seg Out 31, 2011 14:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.