 por Marimar » Qui Nov 03, 2011 14:38
por Marimar » Qui Nov 03, 2011 14:38
Oi pessoal,
Vou tentar explicar o que eu tentei fazer no seguinte exercício, e queria que alguém pudesse me ajudar a concluí-lo.
Admita que, para todo (x,y)
4y. df/dx (x,y) - x df/dy(x,y) = 2
Calcule g' (t), sendo g(t) = f( 2cost, sent).
Chamei x= 2cost y= sent
peguei a equação e integrei 4y e x e deu a seqguinte equação: x^2/2 + 2y^2 = 2
tentei fazer algumas substituições mas nada deu certo, acabei chegando a lugar algum.
se possível, ajudem. Obrigada.
-
Marimar
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Nov 03, 2011 14:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Igor Mirandola » Sex Nov 04, 2011 00:55
por Igor Mirandola » Sex Nov 04, 2011 00:55
Vou supor que f eh uma função de R² em R, isso deveria ficar claro no enunciado...
vou supor ainda que (x,y) leva a f(x,y)...
Admitindo que, para todo (x,y)
4y. df/dx (x,y) - x df/dy(x,y) = 2
Calcule g' (t), sendo g(t) = f( 2cost, sent).
Agora observe que g(t) é uma função R em R, onde para todo t leva-se ao valor g(t), pela lei g(t) = f(2cost, sent), g eh uma composta!
Existe uma função h(t) intermediária, tal que para cada valor de t, eh associado a um h(t) = ( 2cost, sent)
Dessa forma, minha g(t) nada mais é do que uma f(h(t)).
Nesta função x = x(t) e y = y(t)
Acredito que a regra da cadeira será dada por:
dg/dt = df/dx dx/dt + df/dx dy/dt
Podemos determinar dx/dt = d(2cos(t))/dt = - 2 sen(t)
Podemos determinar dy/dt = d(sent)/dt = cos(t)
Assim,
dg/dt = -2 sent df/dx + cost df/dy
Também vamos lembrar que temos por hipotese que 4y. df/dx (x,y) - x df/dy(x,y) = 2
Mas não consigo unir as duas equações!!!
Falta algum dado?
-
Igor Mirandola
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Out 28, 2011 21:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Nov 06, 2011 12:32
por LuizAquino » Dom Nov 06, 2011 12:32
Igor Mirandola escreveu:Assim,
dg/dt = -2 sent df/dx + cost df/dy
Também vamos lembrar que temos por hipotese que 4y. df/dx (x,y) - x df/dy(x,y) = 2
Note que se

e
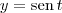
, então:
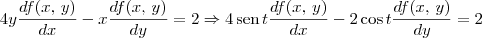
Dividindo esta última equação por -2, note que:
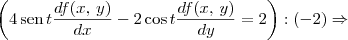

Portanto, podemos concluir que:
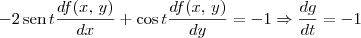
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo II] Regra da cadeia
por carlosmarinio » Qui Nov 03, 2011 15:15
- 2 Respostas
- 2110 Exibições
- Última mensagem por LuizAquino

Dom Nov 06, 2011 20:44
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada - Regra da cadeia
por Sobreira » Dom Dez 02, 2012 13:23
- 1 Respostas
- 2454 Exibições
- Última mensagem por DanielFerreira

Dom Dez 02, 2012 18:05
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2] Regra da cadeia em derivadas parciais
 por NavegantePI » Sáb Jun 25, 2016 18:05
por NavegantePI » Sáb Jun 25, 2016 18:05
- 0 Respostas
- 1984 Exibições
- Última mensagem por NavegantePI

Sáb Jun 25, 2016 18:05
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo de várias variáveis] Problema de regra da cadeia
por Hoteri » Seg Dez 05, 2016 23:56
- 1 Respostas
- 5168 Exibições
- Última mensagem por adauto martins

Qui Dez 08, 2016 09:09
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo II - Regra da Cadeia para várias variáveis
por Guga1981 » Qua Nov 11, 2020 02:22
- 3 Respostas
- 4434 Exibições
- Última mensagem por Guga1981

Dom Nov 22, 2020 05:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e 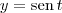 , então:
, então: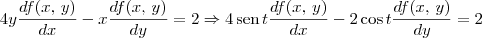
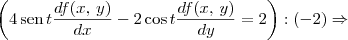

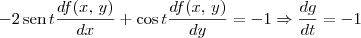

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.