[Gradiente de função de três variáveis]

[dulifs]

Olá,

Fiz o seguinte exercício: Determine um plano que seja tangente a superfície X^2 + 3Y^2 + 2Z^2 = 11/6 e paralelo ao plano X + Y + Z = 10

f ( x, y,z) = ( 2x, 6y, 4z)

Vetor da quação X + Y + Z =10 ==> ( 1,1,1)

(2x,6y,4z) = K (1,1,1)

para K =1

2x=1 x= 1/2

6y=1 y=1/6

4z=1 z=1/4

Montando a equação do plano: (1,1,1)[ ( x - 1/2) + ( y- 1/6) + ( z-1/4) ]
Minha equação do plano deu: X + Y + Z = -11/12

Porém a resposta do livro está X+ Y + Z = -11/6 ou X + Y + Z = 11/6

Creio que errei no vetor, mas se for isso como devo fazer, alguém mais sabe me explicar o que está errado?

muito obrigada, desde já.

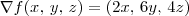
[LuizAquino]

Fiz o seguinte exercício: Determine um plano que seja tangente a superfície X^2 + 3Y^2 + 2Z^2 = 11/6 e paralelo ao plano X + Y + Z = 10

O símbolo correto para o gradiente é o nabla e não o delta como você escreveu. Isto é, a escrita correta é:

Creio que errei no vetor, mas se for isso como devo fazer, alguém mais sabe me explicar o que está errado?

Você obteve que:

(2x, 6y, 4z) = k(1, 1, 1)

A partir disso você (magicamente) fixou k = 1. Aqui está o seu erro.

O correto seria fazer o seguinte.

Da equação acima, você tem que:



Substituindo essas informações na equação da superfície, você tem que:



Agora resolva essa equação.

Em seguida, para cada valor de k obtido você terá um ponto (k/2, k/6, k/4).

Por fim, basta montar a equação de cada plano.