Integral definida[Resolvida]

por **procyon** » Ter Nov 01, 2011 00:34

Olá pessoal, sou novo aqui, já tive uma participação resolvendo uma dúvida de ou outro colega, agora é a minha vez de pedir uma ajuda. É o seguinte, tenho :

$\int_{0}^{1} \frac{x}{\sqrt[2][4 -3x^{4}]} dx$

Não consigo chegar em uma substituição apropriada do tipo u=função que facilite o meu trabalho na integração
Já tentei usar como variável auxiliar u o denominador completo (raíz inclusa) , com o denominador sem a raíz, ou apenas o $u =x^{2} \: \text{transformando a forma} \: 3x^{4} \: \text{em} \; 3 u^{2}$

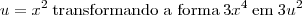
Nenhuma dessas idéias resolveu o meu problema.
Grato.

por **LuizAquino** » Ter Nov 01, 2011 12:21

procyon escreveu:Olá pessoal, sou novo aqui, já tive uma participação resolvendo uma dúvida de ou outro colega, agora é a minha vez de pedir uma ajuda.

Seja bem-vindo ao fórum.

procyon escreveu: $\int_{0}^{1} \frac{x}{\sqrt{4 -3x^{4}}}\,dx$

Não consigo chegar em uma substituição apropriada do tipo u=função que facilite o meu trabalho na integração

Use a substituição trigonométrica $2\,\textrm{sen}\,u = \sqrt{3}x^2$ e $2\cos u \, du = 2\sqrt{3} x \, dx$ .

Com essa substituição, quando x = 0

, note que u = 0

. Já quando x = 1

, note que $u = \frac{\pi}{3}$ .

Dessa forma, temos que:

$\int_{0}^{1} \frac{x}{\sqrt{4 -3x^{4}}}\,dx = \int_0^{\frac{\pi}{3}} \frac{\frac{\cos u}{\sqrt{3}}}{2\cos u}\,du = \int_0^{\frac{\pi}{3}} \frac{1}{2\sqrt{3}}\,du$

Agora termine o exercício.

Observação
Se você desejar revisar a técnica de substituição trigonométrica, então eu recomendo que você assista a vídeo-aula "37. Cálculo I - Integração por Substituição Trigonométrica". Ela está disponível em meu canal no YouTube:

http://www.youtube.com/LCMAquino

por **procyon** » Ter Nov 01, 2011 21:46

por **LuizAquino** » Ter Nov 01, 2011 22:25

procyon escreveu:Encontrei a resposta, desenvolvi o cálculo a partir das seguintes substituicoes:

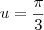$\int_{0}^{1} \frac{x.dx}{\sqrt[2]{4 -3x^{4}}}$

$\int_{0}^{1} \frac{x.dx}{\sqrt[2]{a^{2} - u^{2}}}$

$\nu = \sqrt[2]{3}.x^{2} \:\:\: \text{d}\nu=2x\sqrt[2]{3} \text{dx}$ , a = 2 e ficamos com uma primitiva $(1/a)\textrm{arcsen}\,(u/a)$

Resposta: $\frac{\pi}{6\sqrt{3}}$

Este é um outro caminho igualmente válido. Mas vale lembrar que a primitiva correta é:

$\int {\frac{1}{\sqrt{a^2 - u^2}} \, du = \textrm{arcsen}\,{\frac{u}{a}} + c$

Obviamente, seguindo o caminho que indiquei acima também obtemos a resposta:

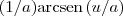
$\int_{0}^{1} \frac{x}{\sqrt{4 -3x^{4}}}\,dx = \int_0^{\frac{\pi}{3}} \frac{1}{2\sqrt{3}}\,du = \left[\frac{u}{2\sqrt{3}}\right]_0^{\frac{\pi}{3}} = \frac{\pi}{6\sqrt{3}}$

Integral definida[Resolvida]

Integral definida[Resolvida]

Integral definida[Resolvida]

Re: Integral definida

Re: Integral definida

Re: Integral definida

Quem está online