ENUNCIADO: DOIS CAPITAIS COLOCADOS, O PRIMEIRO, A 4% a.a., DURANTE 8 MESES, E O SEGUNDO, A 3% a.a., DURANTE 9 MESES, RENDEM JUROS IGUAIS. DETERMINAR ESSES CAPITAIS, SABENDO QUE A SUA DIFERENÇA É DE R$ 12,50.
Pv, Pv1 e Pv2 = VALORES PRESENTES
I = JUROS
i = TAXA DE JUROS
n=NÚMERO DE PERÍODOS
I = Pv.i.n/m
TENTATIVA:
Pv1 - Pv2 = 12,50 => Pv1= Pv2 + 12,50
Pv1* 0,04 / 12 * 8 = Pv2 * 0,03/12 * 9
ENTÃO:
RESOLVENDO A SEGUNDA
Pv1 = Pv2 * 0,8427
SUBSTITUINDO NA PRIMEIRA
Pv2 * 0,8427 = Pv2 + 12,50
RESPOSTA Pv2 = R$ 6,78
ONDE ESTÁ O ERRO !?!?!






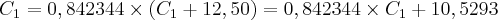


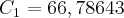
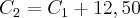 ,
,
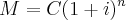
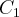 a 4% teremos
a 4% teremos

 a 4% teremos
a 4% teremos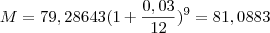



 .
.



