olá boa noite!!
trata de um exercício de permutação de elementos circulares, entretanto ele pede para que a resposta seja dada em porcentagem.
quantos eventos possíveis temos:
PC= (12-1)!= 39916800
Agora vamos ao evento que nos interessa que é quando os meninos estares entre as meninas, ou seja pessoas do mesmo sexo não podem sentar juntas.
são seis meninas e desta forma elas dentro dessa roda poderíam permutar:
PC= (6-1)!= 5! = 120
então poderíamos posicionar estas meninas nessa roda 120 maneiras diferentes.
como os meninos irão ficar entre as meninas então teríamos 6!= 720
pelo principio multiplicativo, teríamos: 120X720= 86400
bem o exercício pede que a resposta seja colocada em porcentagem, correto? então:
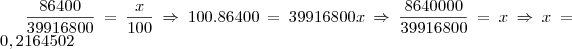
.
Você tem o gabarito da questão, confere aí se estar certo e depois posta. um abraço!!




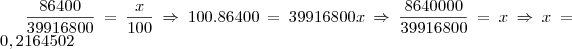 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)