[Geometria Plana] A circunferência e decorrentes

por **mausim** » Ter Out 25, 2011 13:15

Amigos,
'descobri' (assim, entre aspas) uma coisa interessante. Alguém já viu isto? O seguinte:

Temos, para cálculo do comprimento da circunferência, a fórmula

$2 \times \pi \times r$

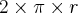
Para o cálculo da área de um círculo,

$\pi \times r ^ 2$

Para o volume da esfera,

${4 \over 3} \times \pi \times r^3$

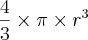
Isto esconde uma evolução. As três fórmulas poderiam (?) ser substituídas por apenas uma fórmula, que é

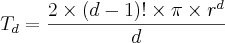${T}_{d} = {{2 \times (d - 1)! \times \pi \times r^d} \over d}}$ (fórmula geral)

onde 'T' seria uma letra qualquer para representar o resultado, 'd' o número de dimensões espaciais da figura e 'r' o raio da figura. Não é necessária uma restrição a 'd', pois não existem dimensões espaciais visíveis menores que 1. A variável 'd', entretanto, tem de pertencer ao conjunto dos números naturais.

Assim, para o comprimento da circunferência, 'd' valeria 1 (Deixemos o 'r' como 'r' mesmo para facilitar a 'descoberta'):

${T}_{1} = {{2 \times (1 - 1)! \times \pi \times r^1} \over 1}}$

Como fatorial de 0 = 1, e reescrevendo, teremos

${T}_{1} = {2 \times \pi \times r}$

que é a fórmula para o comprimento da circunferência.

Da mesma forma, para uma figura de duas dimensões (calculando área) temos

${T}_{2} = {{2 \times (2 - 1)! \times \pi \times r^2} \over 2}}$

Como fatorial de 1 é 1 mesmo e cancelando o denominador com o numerador, temos

${T}_{2} = { \pi \times r^2}}$

Finalmente, para a esfera, um corpo de três dimensões,

${T}_{3} = {{{2 \times (3 - 1)! \times \pi \times r^3} \over 3}}}$

Fatorial de 2 é 2 , o que resulta em

${T}_{3} = {{4 \times \pi \times r^3} \over 3}}$

que é o mesmo de

${T}_{3} = {{{4 \over 3} \times \pi \times r^3} }}$

Quer dizer que a fórmula geral é uma geradora de fórmulas?

Outra coisa, podemos ir além e calcular uma figura hipotética de 4, de 5, de 6, de infinitas dimensões espaciais?

Por exemplo, será que, para 4 dimensões espaciais, algo como

${T}_{4} = 3 \times \pi \times r^4$

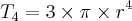
faria sentido matemático, embora não tienha (?) correspondente na natureza?

.

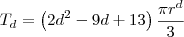
por **luiz_henriquear** » Ter Out 25, 2011 20:17

curti cara,

por **LuizAquino** » Qua Out 26, 2011 09:59

Ao que parece, é apenas uma coincidência. Note que você pode construir várias outras fórmulas que "geram" essas três. Mas essas fórmulas não tem relação geométrica alguma com as figuras originais!

Por exemplo, considere a fórmula:

$T_d = \left(2d^2 - 9d + 13\right)\frac{\pi r^d}{3}$

Substitua d por 1, 2 e 3 e veja o que acontece.

por **mausim** » Qua Out 26, 2011 10:56

LuizAquino escreveu:Ao que parece, é apenas uma coincidência. Note que você pode construir várias outras fórmulas que "geram" essas três. Mas essas fórmulas não tem relação geométrica alguma com as figuras originais!

Por exemplo, considere a fórmula:

$T_d = \left(2d^2 - 9d + 13\right)\frac{\pi r^d}{3}$

Substitua d por 1, 2 e 3 e veja o que acontece.

Luiz Aquino, obrigado por sua intervenção.

Para chegar àquela fórmula, 'fuçando ludicamente' sobre essas relações, eu usei um método um tanto trabalhoso, que consiste em derivar cada fórmula consagrada e verificar a razão que existe entre ela e sua derivada. Achei um padrão.
Depois, comparei cada derivada de uma dimensão com a correspondente anterior. Também achei um outro padrão.

Vi que havia uma ligação entre os padrões que conduzia a uma progressão em fatorial.

Será que por indução matemática ou outra técnica poderia se ter certeza da validade para valores superiores a 3?

grato por mais isto.

por **LuizAquino** » Qua Out 26, 2011 12:24

mausim escreveu:Será que por indução matemática ou outra técnica poderia se ter certeza da validade para valores superiores a 3?

Como eu disse acima, essas "fórmulas" não possuem relação geométrica com as figuras originais. Criá-las é apenas um "passatempo lúdico". Isto é, não faz sentido falar em "validade para valores superiores a 3".

Se quiser outra brincadeira, considere uma fórmula que "gera" a do perímetro e da área do quadrado, bem como a do volume do cubo. Por exemplo, ela poderia ser dada como a seguir, onde l é o lado do quadrado ou a aresta do cubo.

$T_d = \left(3d^2 - 15d + 20\right)\frac{l^d}{2}$

Substitua d por 1, 2 e 3 e veja o que acontece.

por **mausim** » Qua Out 26, 2011 12:39

LuizAquino escreveu:
mausim escreveu:Será que por indução matemática ou outra técnica poderia se ter certeza da validade para valores superiores a 3?

Como eu disse acima, essas "fórmulas" não possuem relação geométrica com as figuras originais. Criá-las é apenas um "passatempo lúdico". Isto é, não faz sentido falar em "validade para valores superiores a 3".

Se quiser outra brincadeira, considere uma fórmula que "gera" a do perímetro e da área do quadrado, bem como a do volume do cubo. Por exemplo, ela poderia ser dada como a seguir, onde l é o lado do quadrado ou a aresta do cubo.

$T_d = \left(3d^2 - 15d + 20\right)\frac{l^d}{2}$

Substitua d por 1, 2 e 3 e veja o que acontece.

Muito obrigado, Luiz Aquino.
Entendi perfeitamente.

[Geometria Plana] A circunferência e decorrentes

[Geometria Plana] A circunferência e decorrentes

[Geometria Plana] A circunferência e decorrentes

Re: [Geometria Plana] A circunferência e decorrentes

Re: [Geometria Plana] A circunferência e decorrentes

Re: [Geometria Plana] A circunferência e decorrentes

Re: [Geometria Plana] A circunferência e decorrentes

Re: [Geometria Plana] A circunferência e decorrentes

Quem está online