Sub-seção para materiais das disciplinas relacionadas à Estatística.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por brunotst » Dom Out 23, 2011 11:34
por brunotst » Dom Out 23, 2011 11:34
Pessoal, estou com a questão abaixo para resolver porém não consigo, me ajudem por favor.
Componentes fabricados por uma determinada indústria foram testados quanto às suas resistências às altas temperaturas e aos pesos que suportam sobre si. Os valores obtidos para essa amostra são os seguintes:
Temperatura: x C o 145 e s C o 19
Peso: x 254Kg e s 23Kg
Verifique em relação a qual desses dois fatores, essa amostra apresentou-se maishomogênea (temperatura ou peso).
-
brunotst
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Ago 01, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Neperiano » Ter Out 25, 2011 16:40
por Neperiano » Ter Out 25, 2011 16:40
Ola
Você tenque ver a relação entre elas, você tenque usar coeficiente de variação de pearson
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por anabatista » Ter Abr 09, 2013 00:17
por anabatista » Ter Abr 09, 2013 00:17
O Coeficiente de Variação de Pearson mede a homogeneidade dos dados
e é calculado À partir da formula:
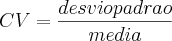
[tex]
E aquele que apresentar menor resultado, será considerado mais homogeneo.
-
anabatista
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Abr 08, 2013 23:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por Pacheco » Ter Out 22, 2013 11:02
por Pacheco » Ter Out 22, 2013 11:02
Por favor vejam se está correto.
Temperatura CV = 0,13%
Peso CV = 0,09%
Peso é o mais homogêneo.
-
Pacheco
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Out 22, 2013 10:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Estatística] Questão de estatistica
por blinkerhope » Dom Out 16, 2011 15:04
- 1 Respostas
- 8880 Exibições
- Última mensagem por Neperiano

Dom Out 16, 2011 17:01
Estatística
-
- [Estatística] Questão de estatística
por antimaxbr » Ter Set 24, 2013 15:02
- 1 Respostas
- 13927 Exibições
- Última mensagem por Paula Laena

Qua Ago 24, 2016 15:55
Estatística
-
- Questão de estatística
por MJC » Ter Mar 17, 2009 12:10
- 0 Respostas
- 1799 Exibições
- Última mensagem por MJC

Ter Mar 17, 2009 12:10
Estatística
-
- Questão de estatística
por gilber » Sáb Jun 13, 2015 10:17
- 0 Respostas
- 4412 Exibições
- Última mensagem por gilber

Sáb Jun 13, 2015 10:17
Estatística
-
- Duvida em questão de estatística
por Jeane25 » Qua Nov 20, 2013 19:34
- 0 Respostas
- 4918 Exibições
- Última mensagem por Jeane25

Qua Nov 20, 2013 19:34
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



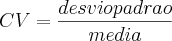 [tex]
[tex]





