Tem 7 maravilhas do mundo antigo e 7 maravilhas do mundo moderno e nenhuma pertence a ambos os conjuntos.Supondo que se escolham ,aleatoriamente,duas entre essa 14 maravilhas.Determine a probabilidade de ambos estarem em um mesmo grupo.(resposta 6/13)
EU TENHO 7/14 PARA SORTEAR 1 DO MESMO GRUPO
PARA SORTEAR DUAS DO MESMO GRUPO, 7/14 x 6/13 = 42/182=21/91=3/13=ERRADO U.U


 ,
, maravilhas.
maravilhas.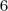 restantes de seu respectivo grupo.
restantes de seu respectivo grupo.
 maravilhas restantes.
maravilhas restantes.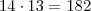



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)