 por rodsales » Dom Abr 26, 2009 14:33
por rodsales » Dom Abr 26, 2009 14:33
A medida do ângulo externo de um polígono regular é 3Pi/5 rad. Quantos lados tem esse polígono?
obs: pensei de todas as maneiras mas não consegui visualizar como fazer, como tenho que estudar sozinho e como não faço cursinho, espero que vcs tenham paciência com minhas dúvidas.
Grato,
Aguardo Respostas...
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por admin » Dom Abr 26, 2009 15:15
por admin » Dom Abr 26, 2009 15:15
Olá
rodsales!
Primeiro certifique-se de identificar corretamente o ângulo externo, eles são suplementares adjacentes aos respectivos ângulos internos, veja na figura:
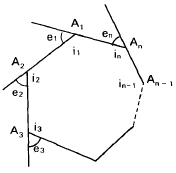
- angulo_externo.jpg (9.02 KiB) Exibido 4880 vezes
Você precisará utilizar que a soma dos ângulos externos de um polígono convexo é:

Tente continuar considerando que a soma dos ângulos externos é:
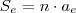
Nota: eu fiz e não obtive

inteiro, o que sugere que este valor do ângulo externo não tenha sido informado corretamente.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Marcampucio » Dom Abr 26, 2009 15:24
por Marcampucio » Dom Abr 26, 2009 15:24

O ângulo externo de um polígono
regular é igual ao seu ângulo interno. A medida do ângulo é dada por

em graus.

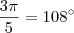
que não é ângulo de polígono regular. Veja:
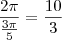
logo há um êrro no seu dado...
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por admin » Dom Abr 26, 2009 15:38
por admin » Dom Abr 26, 2009 15:38
Marcampucio escreveu:O ângulo externo de um polígono regular é igual ao seu ângulo interno.
Olá
Marcampucio!
Como o ângulo externo é suplementar ao interno, eles não seriam iguais apenas para o quadrado?
Contra-exemplos:
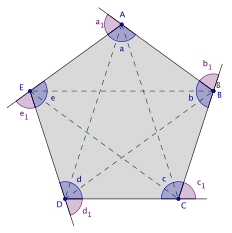
- pentagono_regular.jpg (19.94 KiB) Exibido 6238 vezes

- triangulo.jpg (6.8 KiB) Exibido 6226 vezes
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Marcampucio » Dom Abr 26, 2009 15:54
por Marcampucio » Dom Abr 26, 2009 15:54
Olá fabiosouza,
eu dizia ângulo interno=ângulo central

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por rodsales » Dom Abr 26, 2009 21:04
por rodsales » Dom Abr 26, 2009 21:04
Bem, estou estudando pelo livro "Curso Prático de Matemática", de Paulo Bucchi. É um exercício da pg 348, 24. Quem puder dêem uma olhada. Mesmo assim fico muito grato as respostas de vcs.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





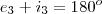



 por
por 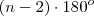 que por sua vez também aceita outra dedução...
que por sua vez também aceita outra dedução... 
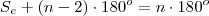

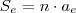
 inteiro, o que sugere que este valor do ângulo externo não tenha sido informado corretamente.
inteiro, o que sugere que este valor do ângulo externo não tenha sido informado corretamente.

 em graus.
em graus.
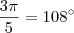 que não é ângulo de polígono regular. Veja:
que não é ângulo de polígono regular. Veja: 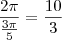




 .
.



