[Geometria] Triângulo ABC

por **Vininhuu** » Sex Out 21, 2011 16:01

Eu precisava de ajuda nesse exercício:

"Seja $\triangle{ABC}$ um triângulo. Mostre que:

a. Se

é um ponto interior de $\triangle{ABC}$ , então $\angle{ACB}<\angle{APB}$ .
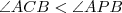b. Se

é um ponto interior de $\triangle{ABC}$ , então AP+BP<AC+BC

.
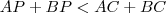c. Se

é um ponto interior de $\triangle{ABC}$ , então AP+BP+CP<AB+AC+BC

. E se

for exterior a $\triangle{ABC}$ ?"

Eu consegui resolver o item a., mas não estou conseguindo resolver os outros...
É que eu precisava entregar a resposta desse exercício no domingo, dia 23/10/2011, mas não estou conseguindo resolver os itens b. e c.
Eu estava pensando em tentar usar o Teorema de Pitágoras, ou alguma coisa assim, mas não consegui encontrar uma jeito de encaixar a soma dos lados no teorema.
Daí eu pensei em tentar provar por absurdo, primeiro mostrando que AP + BP = AC + BC

não é possível, que eu conseguiria provar, porém, eu também tenho que mostrar que AP + BP > AC + BC

não é possível. Coisa que não estou conseguindo fazer :S

Alguém poderia me ajudar, por favor ?
Agradeço !

por **Vininhuu** » Sáb Out 22, 2011 17:07

Vou postar aqui a resolução que eu encontrei do item a.

Usando a imagem abaixo para a melhor visualização da resposta,

: Triângulo ABC.JPG (4.69 KiB) Exibido 2665 vezes

temos que:

$A\hat{B}C + C\hat{A}B + A\hat{C}B = 180^{\circ}$
$A\hat{B}P + P\hat{A}B + A\hat{P}B = 180^{\circ} \rightarrow A\hat{P}B = 180^{\circ} - A\hat{B}P - P\hat{A}B$

O ponto

é interno, então $P\hat{A}B < C\hat{A}B$ e $A\hat{B}P < A\hat{B}C$
$C\hat{A}B = P\hat{A}B + C\hat{A}P$
$A\hat{B}C = A\hat{B}P + P\hat{B}C$

$A\hat{B}C + C\hat{A}B + A\hat{C}B = 180^{\circ}$
$A\hat{B}P + P\hat{B}C + P\hat{A}B + C\hat{A}P + A\hat{C}B = 180^{\circ}$
$A\hat{C}B = 180^{\circ} - A\hat{B}P - P\hat{A}C - P\hat{C}B - C\hat{A}P$
$A\hat{C}B = A\hat{P}B - P\hat{B}C - C\hat{A}P$

Mostrando que $A\hat{P}B > A\hat{C}B$ .

Não sei se isso pode ajudar na resolução dos itens b. e c., mas espero que sim !

Muito obrigado por ao menos lerem

por **dianabarreto** » Sáb Out 22, 2011 20:34

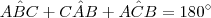
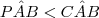olá vininhu. Também sou do PIC e estou com problemas em resolver a parte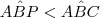

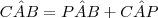
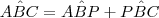
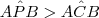da letra c. A letra b se resume ao problema 16, do capítulo 6 do livro do Dmitri Fomin, que você deve ter recebido como material de auxilio pra estudos. vou postar aqui a solução simplificada:

Nesse mesmo triângulo que você desenhou, prolongue o seguimento

até o lado

num ponto

. Agora você irá analisar duas desigualdades:
AC + CD > AD

e

. Some ambas e terá: AC + DC + PD + DB > AD + PB

.

observe que CD + DB = BC

, entao vc terá: AC + BC + PD + > AD + PB

. Subtraia

de cada lado da desigualdade, ficando então com AC + BC > AP + BP

c.q.d.

na letra c, você pode dizer que, com uma analise análoga a que foi feita no item b, tem que: AC + AB > BP + CP

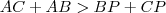e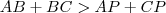

. Você soma as três desigualdades e obtêm que 2AC + 2BC + 2AB > 2AP + 2BP + 2CP

. Aí é só dividir por dois e está provada a proposiçao. Entretanto não consegui mostrar isso para o ponto

exterior a $\triangle ABC$ .

Espero que com o que tenha dito você consiga resolvê-la e postar aqui, já que também preciso. [rs]

por **Vininhuu** » Dom Out 23, 2011 20:50

Diana, me desculpe, mas tentei de todo jeito reponder o resto do item c), mas não consegui :x

Eu inscrevi o $\triangle{ABC}$ em uma circunferência para ver no que dava, tentei usar o Teorema de Pitágoras, tentei encontrar a área dos triângulos encontrados na imagem, mas não encontrei de jeito nenhum );

: Triângulo ABC + Ponto P exterior.JPG (7.05 KiB) Exibido 2636 vezes

Lhe agradeço muito por ter me ajudado nos itens b) e c), mas infelizmente, não pude te ajudar...

Mas, me passe seu msn para nós nos ajudarmos nas tarefas !

Vou conversar com meu P.O. sobre as tarefas do fórum, estão muito difíceis, e nenhuma das tarefas eu consegui responder sem a ajuda de alguém...
Eu só estava tendo a ajuda da minha professora da escola(que não é uma grande ajuda, rs), do meu P.O. (que não conseguiu me ajudar na tarefa 03), e do meu parceiro de encontros presenciais(que também tem um pouco de dificuldade para as respostas das tarefas).
Eu nem tento mais pedir ajuda para os meus colegas de fórum, pois os que conseguem responder são egoístas demais para me darem ao menos uma dica de como devo me posicionar perante ao exercício...
É difícil encontrar um alguém bondoso como você.

Agradeço-te novamente !

Meu msn: vini_demiciano_orsolon@hotmail.com